题目内容
已知椭圆 的左、右焦点分别为
的左、右焦点分别为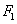 、
、 ,
, 为原点.
为原点.
(1)如图1,点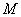 为椭圆
为椭圆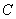 上的一点,
上的一点, 是
是 的中点,且
的中点,且 ,求点
,求点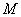 到
到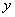 轴的距离;
轴的距离;
(2)如图2,直线 与椭圆
与椭圆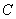 相交于
相交于 、
、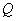 两点,若在椭圆
两点,若在椭圆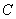 上存在点
上存在点 ,使四边形
,使四边形 为平行四边形,求
为平行四边形,求 的取值范围.
的取值范围.


(1) ;(2)
;(2) .
.
【解析】
试题分析:(1)先设点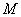 的坐标,并利用点
的坐标,并利用点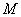 的坐标来表示点
的坐标来表示点 的坐标,利用
的坐标,利用 以及点
以及点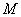 在
在 (2)设
(2)设 ,
, ,
, ,
,
 四边形
四边形 是平行四边形
是平行四边形
 线段
线段 的中点即为线段
的中点即为线段 的中点,即
的中点,即 ,
, ,
,

整理得 代入④式得
代入④式得 ,又
,又 ,
, 或
或 ,
,
 的取值范围是
的取值范围是 .
.
考点:1.直线与椭圆的位置关系;2.韦达定理

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
 ≤2的正整数n的集合为( )
≤2的正整数n的集合为( ) ,an=f(n)(n∈N*),则数列{an}的前n项和Sn的取值范围是________.
,an=f(n)(n∈N*),则数列{an}的前n项和Sn的取值范围是________. (n∈N*),求证:cn+1<cn≤
(n∈N*),求证:cn+1<cn≤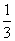 .
. B.
B. C.
C. D.
D.
 、
、 均为单位向量,它们的夹角为
均为单位向量,它们的夹角为 ,那么
,那么 ( )
( ) B.
B. C.
C. D.
D.
 ,则
,则 ”的逆否命题是( )
”的逆否命题是( ) ,则
,则 B.若
B.若 或
或 ,则
,则 D.若
D.若 或
或 ,则
,则 上的函数
上的函数 满足
满足 ,则
,则 .
.