题目内容
已知A(0,1),B(0,-1),C(1,0),动点P满足
•
=2|
|2,则|
+
|的最大值为 .
| AP |
| BP |
| PC |
| AP |
| BP |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:设出P的坐标,由
•
=2|
|2,得出x、y的关系式,求出
+
以及|
+
|的表达式,利用数形结合求出它的最大值.
| AP |
| BP |
| PC |
| AP |
| BP |
| AP |
| BP |
解答:
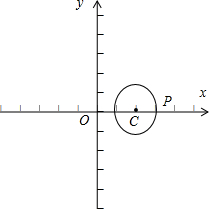 解:设动点P(x,y),
解:设动点P(x,y),
∵A(0,1),B(0,-1),C(1,0),
且
•
=2|
|2,
∴(x,y-1)•(x,y+1)=2[(x-1)2+y2],
即x2+(y2-1)=2x2-4x+2+2y2,
整理,得(x-2)2+y2=1,
∴
+
=(x,y-1)+(x,y+1)=(2x,2y),
∴|
+
|=
=2
;
如图所示,;
∴|
+
|的最大值是2(|OC|+|CP|)=2×(2+1)=6;
故答案为:6.
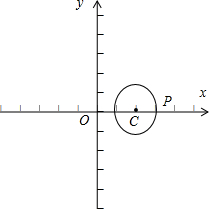 解:设动点P(x,y),
解:设动点P(x,y),∵A(0,1),B(0,-1),C(1,0),
且
| AP |
| BP |
| PC |
∴(x,y-1)•(x,y+1)=2[(x-1)2+y2],
即x2+(y2-1)=2x2-4x+2+2y2,
整理,得(x-2)2+y2=1,
∴
| AP |
| BP |
∴|
| AP |
| BP |
| (2x)2+(2y)2 |
| x2+y2 |
如图所示,;
∴|
| AP |
| BP |
故答案为:6.
点评:本题考查了平面向量的数量积以及数形结合的知识,是基础题.

练习册系列答案
相关题目
收敛数列与发散数列的和数列( )
| A、一定收敛 | B、可能发散 |
| C、一定发散 | D、可能收敛 |
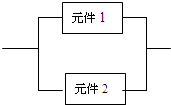 某个部件由两个电子元件按如图连接而成,当元件1或元件2正常工作,该部件正常工作.设两个电子元件的使用寿命(单位:小时)均服从正态分布N(800,100),且各个元件能否正常工作相互独立,那么该部件的使用寿命超过800小时的概率为
某个部件由两个电子元件按如图连接而成,当元件1或元件2正常工作,该部件正常工作.设两个电子元件的使用寿命(单位:小时)均服从正态分布N(800,100),且各个元件能否正常工作相互独立,那么该部件的使用寿命超过800小时的概率为