题目内容
已知数列{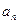 }、{
}、{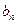 }满足:
}满足: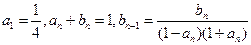 。
。
(Ⅰ)求 ;
;
(Ⅱ)设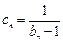 ,求数列
,求数列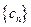 的通项公式;
的通项公式;
(Ⅲ)设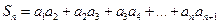 ,不等式
,不等式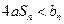 恒成立时,求实数
恒成立时,求实数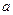 的取值范围。
的取值范围。
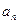 }、{
}、{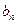 }满足:
}满足: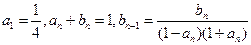 。
。(Ⅰ)求
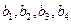 ;
;(Ⅱ)设
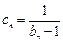 ,求数列
,求数列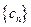 的通项公式;
的通项公式;(Ⅲ)设
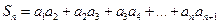 ,不等式
,不等式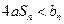 恒成立时,求实数
恒成立时,求实数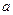 的取值范围。
的取值范围。(Ⅰ)

(Ⅱ)

(Ⅲ)

(Ⅰ)

∵
 ∴
∴ ……4分
……4分(Ⅱ)∵
 ∴
∴ ……5分
……5分∴数列{
 }是以-4为首项,-1为公差的等差数列.
}是以-4为首项,-1为公差的等差数列.∴
 .……7分
.……7分(Ⅲ)由于
 ,所以
,所以 ,从而
,从而 ..……8分
..……8分∴

∴
 ……10分
……10分由条件可知
 恒成立即可满足条件,设
恒成立即可满足条件,设
当
 时,
时, 恒成立
恒成立当
 时,由二次函数的性质知不可能成立
时,由二次函数的性质知不可能成立当
 时,对称轴
时,对称轴 ,
, 在
在 为单调递减函数.
为单调递减函数. ,
,∴
 ∴
∴ 时
时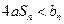 恒成立
恒成立综上知:
 时,
时,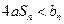 恒成立……14分
恒成立……14分
练习册系列答案
相关题目
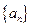 中,
中,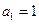 ,
,
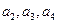 ;(Ⅱ)求数列
;(Ⅱ)求数列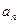 ;
;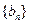 满足
满足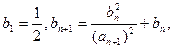
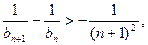 (2)
(2)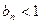
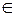
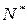 ),其中
),其中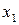 为正实数.
为正实数. 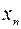 表示xn+1;
表示xn+1;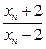 ,证明数列{
,证明数列{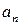 }成等比数列,并求数列{xn}的通项公式;
}成等比数列,并求数列{xn}的通项公式;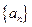 的各项都是正数,
的各项都是正数,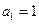 ,
,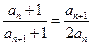 ,
,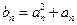 .
.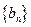 的通项公式;⑵求数列
的通项公式;⑵求数列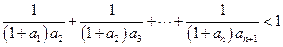 .
.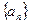 的首项
的首项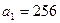 ,前n项和为
,前n项和为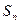 ,且
,且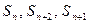 成等差数列.
成等差数列.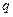 ;
;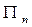 表示
表示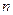 项之积,即
项之积,即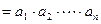 ,试比较
,试比较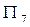 、
、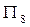 、
、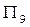 的大小.
的大小.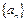 中,
中,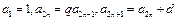 (
(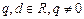 ).
).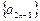 是等比数列,且
是等比数列,且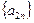 是等差数列,求q, d满足的条件.
是等差数列,求q, d满足的条件.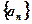 中,
中,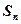 是其前
是其前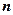 项和,
项和,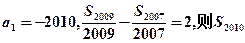 的值为
的值为 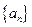 中,
中,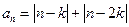 ,若对任意的正整数
,若对任意的正整数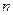 ,
,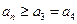 都成立,则
都成立,则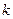 的取值范围为 。
的取值范围为 。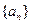 的前
的前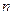 项和为
项和为 ,
,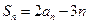 (
(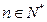 ).
).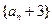 是等比数列,求出数列
是等比数列,求出数列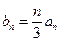 ,求数列
,求数列 的前
的前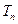 ;
;