题目内容
数列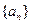 的前
的前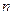 项和为
项和为 ,
,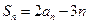 (
(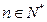 ).
).
(Ⅰ)证明数列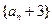 是等比数列,求出数列
是等比数列,求出数列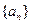 的通项公式;
的通项公式;
(Ⅱ)设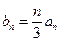 ,求数列
,求数列 的前
的前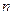 项和
项和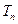 ;
;
(Ⅲ)数列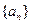 中是否存在三项,它们可以构成等差数列?若存在,求出一组符合条件的项;若不存在,说明理由.
中是否存在三项,它们可以构成等差数列?若存在,求出一组符合条件的项;若不存在,说明理由.
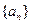 的前
的前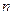 项和为
项和为 ,
,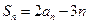 (
(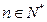 ).
).(Ⅰ)证明数列
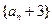 是等比数列,求出数列
是等比数列,求出数列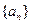 的通项公式;
的通项公式;(Ⅱ)设
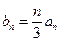 ,求数列
,求数列 的前
的前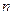 项和
项和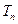 ;
;(Ⅲ)数列
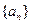 中是否存在三项,它们可以构成等差数列?若存在,求出一组符合条件的项;若不存在,说明理由.
中是否存在三项,它们可以构成等差数列?若存在,求出一组符合条件的项;若不存在,说明理由.(1)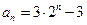 (2)
(2)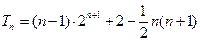 (3)不存在
(3)不存在
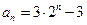 (2)
(2)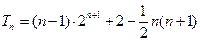 (3)不存在
(3)不存在(Ⅰ)因为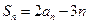 ,所以
,所以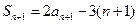 ,
,
则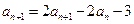 ,所以
,所以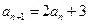 ,
,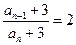 ,
,
数列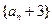 是等比数列,
是等比数列,
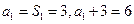 ,
,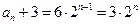 ,
,
所以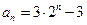 .
.
(Ⅱ)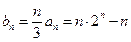 ,
,
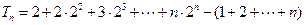 ,
,
令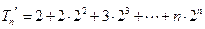 ,①
,①
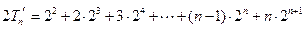 ,②
,②
①-②得,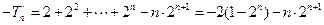 ,
,
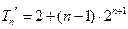 ,
,
所以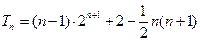 .
.
(Ⅲ)设存在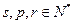 ,且
,且 ,使得
,使得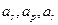 成等差数列,则
成等差数列,则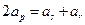 ,
,
即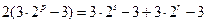 ,
,
即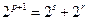 ,
,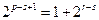 ,
,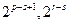 为偶数,而
为偶数,而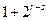 为奇数,
为奇数,
所以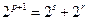 不成立,故不存在满足条件的三项.
不成立,故不存在满足条件的三项.
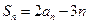 ,所以
,所以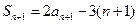 ,
,则
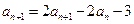 ,所以
,所以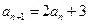 ,
,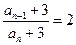 ,
,数列
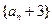 是等比数列,
是等比数列,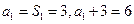 ,
,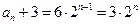 ,
,所以
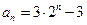 .
.(Ⅱ)
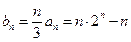 ,
,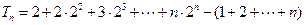 ,
,令
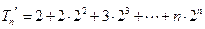 ,①
,①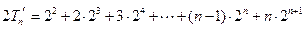 ,②
,②①-②得,
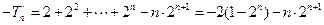 ,
,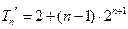 ,
,所以
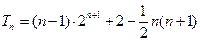 .
.(Ⅲ)设存在
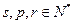 ,且
,且 ,使得
,使得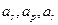 成等差数列,则
成等差数列,则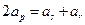 ,
,即
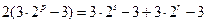 ,
,即
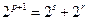 ,
,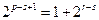 ,
,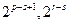 为偶数,而
为偶数,而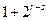 为奇数,
为奇数,所以
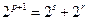 不成立,故不存在满足条件的三项.
不成立,故不存在满足条件的三项.
练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
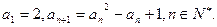
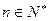 时,恒有
时,恒有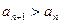 成立;
成立;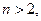 且
且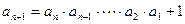 成立;
成立;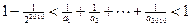 .
.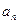 }、{
}、{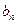 }满足:
}满足: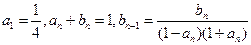 。
。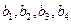 ;
;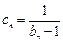 ,求数列
,求数列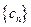 的通项公式;
的通项公式;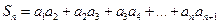 ,不等式
,不等式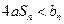 恒成立时,求实数
恒成立时,求实数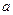 的取值范围。
的取值范围。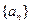 中,已知
中,已知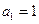 ,且
,且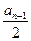 是1与
是1与
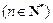 的等差中项.
的等差中项.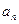 ;
;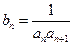 ,记数列
,记数列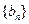 的前
的前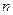 项和为
项和为 ,证明:
,证明: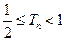
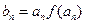 ,记数列
,记数列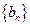 的前n项和为
的前n项和为 ,当
,当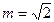 时,求
时,求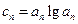 ,问是否存在实数
,问是否存在实数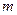 ,使得
,使得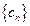 中每一项恒小于它后面的项?若存
中每一项恒小于它后面的项?若存


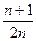
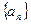 中,前
中,前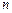 项和为
项和为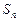 .已知
.已知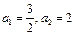 且
且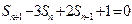 (
(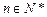 , 且
, 且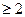 ).(1)求数列
).(1)求数列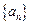 的通项公式;(2)求数列
的通项公式;(2)求数列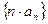 的前
的前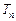 .
.