在△ABC中.已知$a=3\sqrt{3}$.b=4.A=30°.则sinB=$\frac{{2\sqrt{3}}}{9}$．题目和参考答案——青夏教育精英家教网—

题目内容

19．在△ABC中，已知$a=3\sqrt{3}$，b=4，A=30°，则sinB=$\frac{{2\sqrt{3}}}{9}$．

分析由已知利用正弦定理即可计算得解．

解答解：∵$a=3\sqrt{3}$，b=4，A=30°，
∴由正弦定理可得：sinB=$\frac{b•sinA}{a}$=$\frac{4×\frac{1}{2}}{3\sqrt{3}}$=$\frac{{2\sqrt{3}}}{9}$．
故答案为：$\frac{{2\sqrt{3}}}{9}$．

点评本题主要考查了正弦定理在解三角形中的应用，属于基础题．

练习册系列答案

$\frac{{2\sqrt{39}}}{3}$

B．

$\frac{26}{3}\sqrt{3}$

C．

$\frac{8}{3}\sqrt{3}$

D．

$2\sqrt{3}$

10．已知对任意实数x，有f（-x）=-f（x），g（-x）=g（x），且x＜0时，导函数分别满足f′（x）＞0，g′（x）＜0，则x＞0时，成立的是（　　）

7．已知a₁=1，a₂=-$\frac{1}{1+{a}_{1}}$，a₃=-$\frac{1}{1+{a}_{2}}$，…，a_n+1=-$\frac{1}{1+{a}_{n}}$，…．那么a₂₀₁₇=1．

14．已知圆C经过A（3，3），B（2，4）两点，且圆心C在直线y=3x-5上．
（1）求圆C的标准方程；
（2）设P（-m，0），Q（m，0）（m＞0），若圆C上存在点M，使得点M也在以PQ为直径的圆上，求实数m的取值范围．

4．随着我国经济的发展，居民的储蓄款逐年增长，设某地区城乡居民人民币储蓄存款（年底余额）如表：

年份	2010	2011	2012	2013	2014
时间代号t	1	2	3	4	5
储蓄存款y（千亿元）	5	6	7	8	10

（1）取y关于t的回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$t+a；
（2）用所求回归方程预测该地区2015年（t=6）的人民币储蓄存款．

11．求下列函数的导数：
（1）y=（x+1）²（x-1）；
（2）y=x²sin x；
（3）y=$\frac{{e}^{x}+1}{{e}^{x}-1}$
（4）f（x）=$\frac{{e}^{x}}{x-2}$．

8．

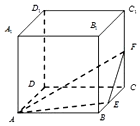如图，在棱长为1的正方体ABCD-A₁B₁C₁D₁中，点E，F分别是棱BC，CC₁的中点，P是侧面BCC₁B₁内一点，若A₁P∥平面AEF，则线段AP长度的取值范围是[$\frac{3\sqrt{2}}{4}$，$\frac{\sqrt{5}}{2}$]．

9．已知向量$\overrightarrow{a}$=（cosα，sinα），$\overrightarrow{b}$=（cosβ，sinβ），α，β∈（0．π）且$\overrightarrow{a}$⊥$\overrightarrow{b}$，求α-β的值．

试题分类