题目内容
(本题满分12分)设函数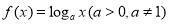 ,
,
(1)若不等式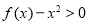 在
在 内恒成立,求
内恒成立,求 的取值范围;
的取值范围;
(2)判断是否存在大于1的实数 ,使得对任意
,使得对任意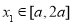 ,都有
,都有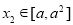 满足等式:
满足等式: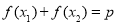 ,且满足该等式的常数
,且满足该等式的常数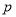 的取值唯一?若存在,求出所有符合条件的
的取值唯一?若存在,求出所有符合条件的 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(1) ;(2)存在大于1的实数2满足条件.
;(2)存在大于1的实数2满足条件.
【解析】
试题分析:(1)不等式 在
在 内恒成立,所以在
内恒成立,所以在 内
内 图像在
图像在 图像的上方,
图像的上方,
∴ ,可得
,可得 ;
;
(2)假设存在大于1的实数 满足条件,
满足条件,
由 ,即
,即 ,∴
,∴ ,
,
把 看作
看作 的函数
的函数 ,其在区间
,其在区间 上单调递减,∴
上单调递减,∴ 时,
时, ,
,
∴ ,∴
,∴ ,
,
因为常数 的取值唯一,所以
的取值唯一,所以 ,∴
,∴ .
.
所以存在大于1的实数 ,且
,且 .
.
考点:函数的单调性,恒成立问题

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
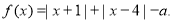
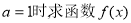 的最小值;
的最小值;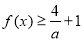 对任意的实数
对任意的实数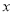 恒成立,求实数
恒成立,求实数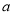 的取值范围.
的取值范围. ,
, 是定义在R上的奇函数,当
是定义在R上的奇函数,当 时,
时, ,则函数
,则函数 的大致图象为( )
的大致图象为( )

 +
+ =1与双曲线
=1与双曲线 -
- =1(m,n,p,q∈R+)有共同的焦点F1、F2,P是椭圆和双曲线的一个交点,则|PF1|·|PF2|= 。
=1(m,n,p,q∈R+)有共同的焦点F1、F2,P是椭圆和双曲线的一个交点,则|PF1|·|PF2|= 。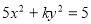 的一个焦点是(0,2),那么
的一个焦点是(0,2),那么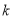 等于 ( )
等于 ( ) C.1 D.
C.1 D.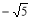
 ,已知函数
,已知函数 的定义域为集合
的定义域为集合 ,函数
,函数 的值域为集合
的值域为集合 ,
,  ;
; 且
且 ,求实数
,求实数 的取值范围.
的取值范围. 的大致图像是( )
的大致图像是( ) 
 为偶函数且
为偶函数且 ,又
,又 ,函数
,函数 ,若
,若 恰好有2个零点,则
恰好有2个零点,则 .
.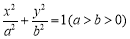 的焦距为
的焦距为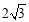 ,且经过点
,且经过点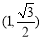 .
.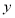 轴正半轴的交点, 椭圆Ω上是否存在两点M、N,使得△AMN是以A为直角顶点的等腰直角三角形?若存在,请说明有几个;若不存在,请说明理由.
轴正半轴的交点, 椭圆Ω上是否存在两点M、N,使得△AMN是以A为直角顶点的等腰直角三角形?若存在,请说明有几个;若不存在,请说明理由.