题目内容
若命题p“不等式|x|≥m-1的解集为R”是命题q“f(x)=(5-2m+a)x是增函数”的充分而不必要条件,求实数m的取值范围.
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:先化简p,q再根据命题p是命题q充分而不必要条件,得到p的解集的范围应该比q的解集的范围小,问题得以解决
解答:
解:∵不等式|x|≥m-1的解集为R,
∴m-1≤0,解得m≤1,即p:m≤1.
∵f(x)=(5-2m)x是(-∞,+∞)上的增函数,
∴5-2m+a>1,解得m<
a+2,即q:m<
a+2.
∵命题p是命题q充分而不必要条件,
∴p⇒q,q不能推出p,
∴p的解集的范围应该比q的解集的范围小,
∴m≤1
∴m-1≤0,解得m≤1,即p:m≤1.
∵f(x)=(5-2m)x是(-∞,+∞)上的增函数,
∴5-2m+a>1,解得m<
| 1 |
| 2 |
| 1 |
| 2 |
∵命题p是命题q充分而不必要条件,
∴p⇒q,q不能推出p,
∴p的解集的范围应该比q的解集的范围小,
∴m≤1
点评:本题主要考查充分条件、必要条件、充要条件的定义,属于基础题.

练习册系列答案
相关题目
已知抛物线C:y2=4x,点P(m,0),O为坐标原点,若在抛物线C上存在一点Q,使得∠OQP=90°,则实数m的取值范围是( )
| A、(4,8) |
| B、(4,+∞) |
| C、(0,4) |
| D、(8,+∞) |
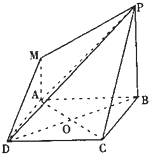 如图,四边形ABCD是正方形,MA⊥平面ABCD,MA∥PB,PB=AB=2MA=2.
如图,四边形ABCD是正方形,MA⊥平面ABCD,MA∥PB,PB=AB=2MA=2.
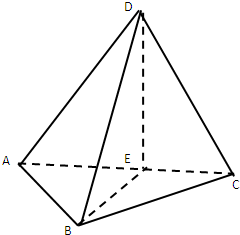 如图,三棱锥D-ABC中,AB=BC=2,BD=3,∠ABC=∠DBA=∠DBC=60°,E为AC的中点.
如图,三棱锥D-ABC中,AB=BC=2,BD=3,∠ABC=∠DBA=∠DBC=60°,E为AC的中点.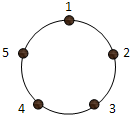 如图,圆周上按顺时针方向标有1,2,3,4,5五个点,一只青蛙按瞬时针方向绕圆从一个点跳到下一个点.若它停在奇数点上,则下一次只能跳一个点,若停在偶数点上,则可以连续跳2个点.该青蛙从5这点起跳,经2009次跳后它将停在的点是( )
如图,圆周上按顺时针方向标有1,2,3,4,5五个点,一只青蛙按瞬时针方向绕圆从一个点跳到下一个点.若它停在奇数点上,则下一次只能跳一个点,若停在偶数点上,则可以连续跳2个点.该青蛙从5这点起跳,经2009次跳后它将停在的点是( )