题目内容
数列{（-1）nn}的前2k-1项之和S2k-1（k∈N*）为：
- A.3k-2
- B.-k
- C.
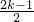
- D.2-3k
B
分析：先把S2k-1中的项，每两项一组，发现相邻两项之和为1，进而可知S2k-1=（k-1）×1-（2k-1）答案可得．
解答：S2k-1=（-1+2）+（-3+4）…+（-2k+3+2k-2）-（2k-1）=k-1-2k+1=-k
故选B
点评：本题主要考查了数列的求和．解题的关键是利用了相邻两项知和为1，对数列进行分组求和．
分析：先把S2k-1中的项，每两项一组，发现相邻两项之和为1，进而可知S2k-1=（k-1）×1-（2k-1）答案可得．
解答：S2k-1=（-1+2）+（-3+4）…+（-2k+3+2k-2）-（2k-1）=k-1-2k+1=-k
故选B
点评：本题主要考查了数列的求和．解题的关键是利用了相邻两项知和为1，对数列进行分组求和．
练习册系列答案
小学教材全测系列答案
小学数学口算题卡脱口而出系列答案
优秀生应用题卡口算天天练系列答案
浙江之星课时优化作业系列答案
相关题目