题目内容
17.已知数列{an}满足a1=1,${a_{n+1}}=\frac{a_n}{{2{a_n}+1}},n∈{N^*}$.(1)证明:数列$\{\frac{1}{a_n}\}$是等差数列,并求数列{an}的通项公式;
(2)设${b_n}=\frac{a_n}{2n+1}$,数列{bn}的前n项和为Sn,求使不等式Sn<k对一切n∈N*恒成立的实数k的范围.
分析 (1)对递推式两边取倒数化简即可得出$\frac{1}{{a}_{n+1}}-\frac{1}{{a}_{n}}$=2,结论得证,利用等差数列的通项公式得出$\frac{1}{{a}_{n}}$,再得出an;
(2)使用裂项法求出Sn,使用不等式得出Sn的范围,从而得出k的范围.
解答 (1)证明:∵${a_{n+1}}=\frac{a_n}{{2{a_n}+1}}$,∴$\frac{1}{{{a_{n+1}}}}=\frac{1}{a_n}+2$,
即$\frac{1}{{a}_{n+1}}-\frac{1}{{a}_{n}}$=2,又a1=1,
∴数列$\left\{{\frac{1}{a_n}}\right\}$是以1为首项,2为公差的等差数列,
∴$\frac{1}{a_n}=2n-1$,
∴${a_n}=\frac{1}{2n-1}$.
(2)解:${b_n}=\frac{1}{(2n+1)(2n-1)}=\frac{1}{2}(\frac{1}{2n-1}-\frac{1}{2n+1})$,
∴${S_n}=\frac{1}{2}[(1-\frac{1}{3})+(\frac{1}{3}-\frac{1}{5})+…+(\frac{1}{2n-1}-\frac{1}{2n+1})]$=$\frac{1}{2}(1-\frac{1}{2n+1})<\frac{1}{2}$,
要使不等式Sn<k对一切n∈N*恒成立,则k$≥\frac{1}{2}$.
∴k的范围为$[{\frac{1}{2},+∞})$.
点评 本题考查了等差数列的判断,等差数列的通项公式,裂项法求和,属于中档题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
8.已知集合A={0,1,2,3,4,5},集合$B=\{x∈N,\frac{x-4}{x}≤0\}$,则∁AB=( )
| A. | {5} | B. | {0,5} | C. | {1,5} | D. | {0,4,5} |
6.设a=log54,b=log53,c=log45,则( )
| A. | a<c<b | B. | b<c<a | C. | a<b<c | D. | b<a<c |
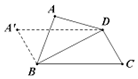 如图,矩形ABCD中,AB=1,BC=$\sqrt{3}$,将△ABD沿对角线BD向上翻折,若翻折过程中AC长度在[$\frac{\sqrt{10}}{2}$,$\frac{\sqrt{13}}{2}$]内变化,则点A所形成的运动轨迹的长度为$\frac{\sqrt{3}π}{12}$.
如图,矩形ABCD中,AB=1,BC=$\sqrt{3}$,将△ABD沿对角线BD向上翻折,若翻折过程中AC长度在[$\frac{\sqrt{10}}{2}$,$\frac{\sqrt{13}}{2}$]内变化,则点A所形成的运动轨迹的长度为$\frac{\sqrt{3}π}{12}$.