题目内容
9.已知双曲线C:4x2-y2=4及直线l:y=kx-1(1)求双曲线C的渐近线方程及离心率;
(2)直线l与双曲线C左右两支各有一个公共点,求实数k的取值范围.
分析 (1)由题意可知:${x}^{2}-\frac{{y}^{2}}{4}=1$,可知焦点在x轴上,则a=1,b=2,c=$\sqrt{4+1}$=$\sqrt{5}$,渐近线方程为y=±$\frac{b}{a}$x=±2x,离心率为e=$\frac{c}{a}$=$\sqrt{5}$;
(2)将直线方程代入椭圆方程,由韦达定理可知:x1•x2=-$\frac{5}{4-{k}^{2}}$,直线l与双曲线C左右两支各有一个公共点,$\left\{\begin{array}{l}{4-{k}^{2}≠0}\\{△=(2k)^{2}-4(4-{k}^{2})(-5)>0}\\{{x}_{1}{x}_{2}=\frac{-5}{4-{k}^{2}}<0}\end{array}\right.$,即可求得k的取值范围.
解答 解:(1)将双曲线C:4x2-y2=4,化为标准方程得${x}^{2}-\frac{{y}^{2}}{4}=1$,可知焦点在x轴上,
则a=1,b=2,c=$\sqrt{4+1}$=$\sqrt{5}$,
∴双曲线的渐近线方程为y=±$\frac{b}{a}$x=±2x,
离心率为e=$\frac{c}{a}$=$\sqrt{5}$,(4分)
(2)由直线l:y=kx-1,直线l与双曲线C相交于A,B两点,设A(x1,y1),B(x2,y2),
则$\left\{\begin{array}{l}{y=kx-1}\\{4{x}^{2}-{y}^{2}=4}\end{array}\right.$,消去y,整理得:(4-k2)x2+2kx-5=0,
由韦达定理可知:x1•x2=-$\frac{5}{4-{k}^{2}}$(6分)
直线l与双曲线C左右两支各有一个公共点,
$\left\{\begin{array}{l}{4-{k}^{2}≠0}\\{△=(2k)^{2}-4(4-{k}^{2})(-5)>0}\\{{x}_{1}{x}_{2}=\frac{-5}{4-{k}^{2}}<0}\end{array}\right.$,(8分)
解得:k2<5,且k2<4,
∴-2<k<2,
∴实数k的取值范围是(-2,2)…12分
点评 本题考查双曲线的标准方程及简单几何性质,考查直线与双曲线位置关系,直线与双曲线的交点问题,考查计算能力,属于中档题.

 名校课堂系列答案
名校课堂系列答案| A. | -1 | B. | 1 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
| A. | y=3x-8 | B. | y=-3x+8 | C. | y=3x-10 | D. | y=-3x+10 |
| A. | f(sin$\frac{π}{8}$)<f(cos$\frac{π}{8}$) | B. | f(sin1)>f(cos1) | ||
| C. | f(sin$\frac{π}{12}$)<f(sin$\frac{5π}{12}$) | D. | f(sin$\frac{π}{12}$)>f(tan$\frac{π}{12}$) |
| A. | 243 | B. | $27\root{5}{27}$ | C. | $\sqrt{3}$ | D. | 81 |
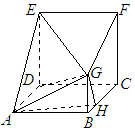 在多面体ABCDEFG中,四边形ABCD与CDEF是边长均为a正方形,CF⊥平面ABCD,BG⊥平面ABCD,且AB=2BG=4BH
在多面体ABCDEFG中,四边形ABCD与CDEF是边长均为a正方形,CF⊥平面ABCD,BG⊥平面ABCD,且AB=2BG=4BH