题目内容
设an=(1-
)(1-
)(1-
)…(1-
)(n∈N,且n≥2)
(1)求a2,a3,a4,猜想an的化简式;
(2)用数学归纳法证明(1)的结果;
(3)设正数数列{bn}满足b1=1,bn2=2(an-
),求证:n>1时,b1+b2+b3+…+bn>
.
| 1 |
| 4 |
| 1 |
| 9 |
| 1 |
| 16 |
| 1 |
| n2 |
(1)求a2,a3,a4,猜想an的化简式;
(2)用数学归纳法证明(1)的结果;
(3)设正数数列{bn}满足b1=1,bn2=2(an-
| 1 |
| 2 |
| n |
考点:数学归纳法
专题:综合题,点列、递归数列与数学归纳法
分析:(1)代入计算,即可求a2,a3,a4,猜想an的化简式;
(2)用数学归纳法证明,关键是证明n=k+1时,结论成立;
(3)bn2=2(an-
)=
,可得bn=
,利用放缩法,即可证明结论.
(2)用数学归纳法证明,关键是证明n=k+1时,结论成立;
(3)bn2=2(an-
| 1 |
| 2 |
| 1 |
| n |
| 1 | ||
|
解答:
(1)解:a2=
,a3=(1-
)(1-
)=
=
,a4=(1-
)(1-
)(1-
)=
,
猜想an=
(n∈N,且n≥2);
(2)证明:①n=2时,结论成立;
②假设n=k时成立,即ak=
,
则n=k+1时,ak+1=
•[1-
]=
,成立,
∴an=
(n∈N,且n≥2);
(3)证明:bn2=2(an-
)=
,∴bn=
,
∴n>1时,b1+b2+b3+…+bn>1+
+…+
>
=
| 3 |
| 4 |
| 1 |
| 4 |
| 1 |
| 9 |
| 2 |
| 3 |
| 4 |
| 6 |
| 1 |
| 4 |
| 1 |
| 9 |
| 1 |
| 16 |
| 5 |
| 8 |
猜想an=
| n+1 |
| 2n |
(2)证明:①n=2时,结论成立;
②假设n=k时成立,即ak=
| k+1 |
| 2k |
则n=k+1时,ak+1=
| k+1 |
| 2k |
| 1 |
| (k+1)2 |
| k+2 |
| 2(k+1) |
∴an=
| n+1 |
| 2n |
(3)证明:bn2=2(an-
| 1 |
| 2 |
| 1 |
| n |
| 1 | ||
|
∴n>1时,b1+b2+b3+…+bn>1+
| 1 | ||
|
| 1 | ||
|
| n | ||
|
| n |
点评:本题考查数学归纳法,考查不等式的证明,考查学生分析解决问题的能力,考查数列的通项,属于中档题.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
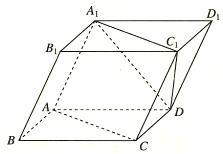 如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC=∠A1AC=60°,平面AA1CC1⊥平面ABCD.
如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC=∠A1AC=60°,平面AA1CC1⊥平面ABCD.