题目内容
16.已知函数f(x)是定义在R上的奇函数,当x≤0时,f(x)=x(1-x),若数列{an}满足a1=$\frac{1}{2}$,且an+1=$\frac{1}{1-{a}_{n}}$,则f(a2015)+f(a2016)=( )| A. | -8 | B. | 8 | C. | -4 | D. | 4 |
分析 根据条件设x>0,从而有-x<0,这样即可求出f(x)=x(1+x),根据${a}_{1}=\frac{1}{2}$,且${a}_{n+1}=\frac{1}{1-{a}_{n}}$可求数列{an}的前四项,从而会发现该数列是以3为周期的周期数列,这样便可以求出a2015和a2016的值,从而可求出f(a2015)+f(a2016)的值.
解答 解:设x>0,则-x<0;
∵f(x)是定义在R上的奇函数;
∴f(x)=-f(-x)=-[-x(1+x)]=x(1+x);
由${a}_{1}=\frac{1}{2}$,且${a}_{n+1}=\frac{1}{1-{a}_{n}}$得:
${a}_{2}=\frac{1}{1-{a}_{1}}=\frac{1}{1-\frac{1}{2}}=2$,${a}_{3}=\frac{1}{1-{a}_{2}}=\frac{1}{1-2}=-1$,${a}_{4}=\frac{1}{1-{a}_{3}}=\frac{1}{1-(-1)}=\frac{1}{2}$,…;
∴数列{an}是以3为周期的周期数列;
∴a2015=a671×3+2=a2=2,a2016=a671×3+3=a3=-1;
∴f(a2015)+f(a2016)=f(2)+f(-1)=2(1+2)+(-1)(1+1)=4.
故选:D.
点评 考查奇函数的定义,对于奇函数,已知一区间上的解析式,而求其对称区间上的解析式的方法,根据数列的首项和递推公式可以求该数列的前几项,以及周期数列的概念,已知函数求值的方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.设a,b∈R,且b>1是“a+b>2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
1.如图,为一个半圆柱和一个半圆锥拼接而成的组合体的三视图,则该组合体的体积为( )
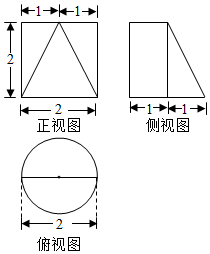

| A. | $\frac{8π}{3}$ | B. | $\frac{4π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{3}$ |
5.若[x]表示不超过x的最大整数,则下面的程序框图运行之后输出的结果为( )


| A. | 48920 | B. | 49660 | C. | 49800 | D. | 51867 |
6.定义集合A?B={x|x∈A或x∈B且x∉A∩B},设全集U={x|1<x<10},集合A={x|2<x<6},B={x|5<x<7},则(∁UA)?B=( )
| A. | [6,7) | B. | (1,2]∪(5,6)∪[7,10) | C. | (1,6) | D. | (1,2]∪(5,6]∪(7,10) |
 已知p,m>0,抛物线E:x2=2py上一点M(m,2)到抛物线焦点F的距离为$\frac{5}{2}$.
已知p,m>0,抛物线E:x2=2py上一点M(m,2)到抛物线焦点F的距离为$\frac{5}{2}$.