题目内容
18.已知实数x,y满足$\left\{\begin{array}{l}{x+y-5≤0}\\{2x-y+2≥0}\\{y≥0}\end{array}\right.$,则目标函数z=x-y的最小值为-3.分析 作出不等式组对应的平面区域,利用z的几何意义进行求解即可.
解答  解:作作出不等式组对应的平面区域如图:
解:作作出不等式组对应的平面区域如图:
由z=x-y,得y=x-z表示,斜率为1纵截距为-z的一组平行直线,
平移直线y=x-z,当直线经过点A时,此时直线y=x-z截距最大,z最小.
由$\left\{\begin{array}{l}{x+y-5=0}\\{2x-y+2=0}\end{array}\right.$,得$\left\{\begin{array}{l}{x=1}\\{y=4}\end{array}\right.$,
此时zmin=1-4=-3.
故答案为:-3.
点评 本题主要考查线性规划的基本应用,利用z的几何意义是解决线性规划问题的关键,注意利用数形结合来解决.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
6.某四棱锥的三视图如图所示,则该四棱锥的侧面积是( )
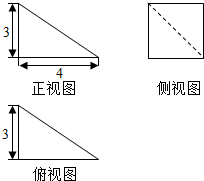

| A. | 27 | B. | 30 | C. | 32 | D. | 36 |
13.下列命题错误的是( )
| A. | 命题“若m>0,则方程x2+x-m=0有实根”的逆否命题为:“若方程x2+x-m=0无实根,则m≤0” | |
| B. | 若p∧q为假命题,则p,q均为假命题 | |
| C. | “x=1”是“x2-3x+2=0”的充分不必要条件 | |
| D. | 若椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{25}$=1的两焦点为F1、F2,且弦AB过F1点,则△ABF2的周长为20 |
3.下列函数中,是偶函数且在区间(0,+∞)上单调递减的函数是( )
| A. | y=2x | B. | y=$\sqrt{x}$ | C. | y=|x| | D. | y=-x2+1 |
10.已知复数z满足zi=1,则|z|=( )
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | $\frac{1}{2}$ |
7.定义平面上一点P到曲线C的距离为点P到曲线C上所有点距离的最小值,那么平面内到定圆的距离与到定点A的距离相等的点的轨迹不可能是( )
| A. | 圆 | B. | 椭圆 | C. | 双曲线的一支 | D. | 直线 |
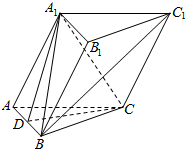 在三棱柱ABC-A1B1C1中,AA1⊥BC,∠A1AC=60°,AA1=AC=BC=$\sqrt{2}$,A1B=2.
在三棱柱ABC-A1B1C1中,AA1⊥BC,∠A1AC=60°,AA1=AC=BC=$\sqrt{2}$,A1B=2.