题目内容
f(x)是定义在D上的函数,若存在区间[m,n]⊆D,使函数f(x)在[m,n]上的值域恰为[km,kn],则称函数f(x)是k型函数.给出下列说法:
①f(x)=3-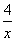 不可能是k型函数;
不可能是k型函数;
②若函数y=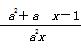 (a≠0)是1型函数,则n-m的最大值为
(a≠0)是1型函数,则n-m的最大值为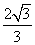 ;
;
③若函数y=-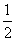 x2+x是3型函数,则m=-4,n=0;
x2+x是3型函数,则m=-4,n=0;
④设函数f(x)=x3+2x2+x(x≤0)是k型函数,则k的最小值为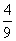 .
.
其中正确的说法为________.(填入所有正确说法的序号)
②③
[解析] 对于①,注意到函数f(x)=3-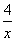 在[2,4]上的值域是[1,2]=
在[2,4]上的值域是[1,2]=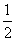 ×2,
×2,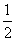 ×4,因此函数f(x)=3-
×4,因此函数f(x)=3-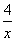 可能是k型函数,故①不正确;对于②,依题意得函数y=
可能是k型函数,故①不正确;对于②,依题意得函数y=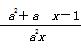 =
= -
-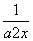 ,存在区间[m,n],
,存在区间[m,n],
使函数y= -
-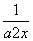 在[m,n]上的值域恰为[m,n],注意到函数y=
在[m,n]上的值域恰为[m,n],注意到函数y= -
-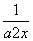 在区间[m,n]上是增函数,于是有
在区间[m,n]上是增函数,于是有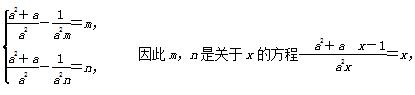 即a2x2-(a2+a)x+1=0的两个不等的实根,
即a2x2-(a2+a)x+1=0的两个不等的实根,
则m+n= ,mn=
,mn=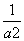 ,
,
从而n-m
= 的最大值是
的最大值是 =
=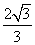 ,因此②正确;对于③,依题意得存在区间[m,n],使得函数y=-
,因此②正确;对于③,依题意得存在区间[m,n],使得函数y=-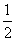 x2+x在区间[m,n]上的值域是[3m,3n],注意到y=-
x2+x在区间[m,n]上的值域是[3m,3n],注意到y=-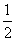 x2+x=-
x2+x=-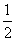 (x-1)2+
(x-1)2+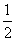 ≤
≤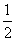 ,因此3n≤
,因此3n≤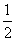 ,n≤
,n≤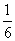 ,函数y=-
,函数y=-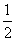 x2+x在区间[m,n]上是增函数,
x2+x在区间[m,n]上是增函数,
于是有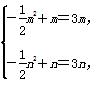
即m,n是方程-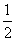 x2+x=3x的两个实根-4,0,又m<n,因此m=-4,n=0,故③正确;对于④,当x≤0时,f′(x)=3x2+4x+1=(3x+1)(x+1),若-
x2+x=3x的两个实根-4,0,又m<n,因此m=-4,n=0,故③正确;对于④,当x≤0时,f′(x)=3x2+4x+1=(3x+1)(x+1),若- <x<0,则f′(x)>0;若-1<x<-
<x<0,则f′(x)>0;若-1<x<- ,则f′(x)<0,函数f(x)=x3+2x2+x(x≤0)在
,则f′(x)<0,函数f(x)=x3+2x2+x(x≤0)在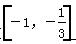 上是减函数,在
上是减函数,在 上是增函数,且
上是增函数,且 =-
=-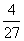 ,f(-1)=f(0)=0,因此当x∈[-1,0]时,f(x)相应的值域是
,f(-1)=f(0)=0,因此当x∈[-1,0]时,f(x)相应的值域是 注意到
注意到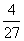 <
<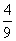 ,因此④不正确.综上,其中正确的说法为②③.
,因此④不正确.综上,其中正确的说法为②③.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
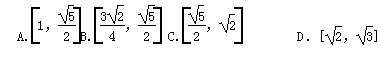
 ln(1-x)的定义域是( )
ln(1-x)的定义域是( )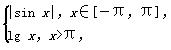
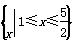 上的两个函数.对任意的x∈M,存在常数x0∈M,使得f(x)≥f(x0),g(x)≥g(x0),且f(x0)=g(x0).则函数f(x)在集合M上的最大值为( )
上的两个函数.对任意的x∈M,存在常数x0∈M,使得f(x)≥f(x0),g(x)≥g(x0),且f(x0)=g(x0).则函数f(x)在集合M上的最大值为( ) B.4
B.4 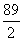
 的前n项和为Sn,若S2n+1-Sn≤
的前n项和为Sn,若S2n+1-Sn≤ 对n∈N*恒成立,则正整数m的最小值是________.
对n∈N*恒成立,则正整数m的最小值是________.