题目内容
对于集合A={a1,a2,…,an}(n∈N*,n≥3),定义集合S={x|x=ai+aj,1≤i<j≤n},记集合S中的元素个数为S(A).若a1,a2,…,an是公差大于零的等差数列,则S(A)=________.
2n-3
[解析] 由题意,集合S中最小项为a1+a2=2a1+d,最大项为an-1+an=2a1+(2n-3)d,对任意的i(1≤i≤2n-3),如果i≤n-1,则可取2a1+id=a1+(a1+id)=a1+ai+1∈S,若n≤i≤2n-3,可取2a1+id=a1+(n-1)d+a1+(i-n+1)d=an+ai-n+2,显然由于n≤i≤2n-3,有2≤i-n+2≤n-1,即2a1+id∈S,所以S(A)=2n-3.

练习册系列答案
相关题目
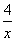 不可能是k型函数;
不可能是k型函数;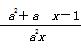 (a≠0)是1型函数,则n-m的最大值为
(a≠0)是1型函数,则n-m的最大值为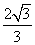 ;
;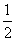 x2+x是3型函数,则m=-4,n=0;
x2+x是3型函数,则m=-4,n=0;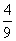 .
.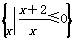 ,则集合∁UA等于( )
,则集合∁UA等于( )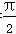 +kπ,y≠
+kπ,y≠
 为偶函数,
为偶函数, 为奇函数,其中
为奇函数,其中 、
、 为常数,则
为常数,则 _____________
_____________