题目内容
如图,将正方形 沿对角线
沿对角线 折起,使平面
折起,使平面 平面
平面 ,
, 是
是 的中点,那么异面直线
的中点,那么异面直线 、
、 所成的角的正切值为 。
所成的角的正切值为 。

 沿对角线
沿对角线 折起,使平面
折起,使平面 平面
平面 ,
, 是
是 的中点,那么异面直线
的中点,那么异面直线 、
、 所成的角的正切值为 。
所成的角的正切值为 。

取 中点
中点 ,连接
,连接 。因为
。因为 分别是
分别是 中点,所以
中点,所以 ,则
,则 是异面直线
是异面直线 和
和 所成角。因为
所成角。因为 是正方形,设其边长为1,则
是正方形,设其边长为1,则 ,
, 。因为平面
。因为平面 平面
平面 ,所以
,所以 平面
平面 ,从而有
,从而有 。因为
。因为 ,所以
,所以
 中点
中点 ,连接
,连接 。因为
。因为 分别是
分别是 中点,所以
中点,所以 ,则
,则 是异面直线
是异面直线 和
和 所成角。因为
所成角。因为 是正方形,设其边长为1,则
是正方形,设其边长为1,则 ,
, 。因为平面
。因为平面 平面
平面 ,所以
,所以 平面
平面 ,从而有
,从而有 。因为
。因为 ,所以
,所以

练习册系列答案
相关题目
 中(图1),
中(图1), 是
是 的中点,
的中点, ,
,
 ,
, 将(图1)沿直线
将(图1)沿直线 折起,使二面角
折起,使二面角 为
为 (如图2)
(如图2) 平面
平面 ;
; 与
与 所成角的余弦值;
所成角的余弦值; 到平面
到平面 的距离.
的距离.
 中,已知
中,已知 ,
, ,
, .
. 与底面
与底面 所成角正切值;
所成角正切值; (不包含端点)上确定一点
(不包含端点)上确定一点 的位置,
的位置, (要求说明理由);
(要求说明理由); ,求二面角
,求二面角 的大小.
的大小.

 中,
中, 是
是 的中点。
的中点。 上求一点
上求一点 ,使
,使 平面
平面 ;
; 的余弦值.
的余弦值.
 ,对任意
,对任意 ,试判断
,试判断 的形状;
的形状; 中,
中, ,
, 为
为 的中点,
的中点, 交
交 于
于 ,求证:
,求证: .
.
 中,
中, ,
, ,点
,点 在
在 上且
上且 (如图(3)).把
(如图(3)).把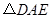 沿
沿 向上折起到
向上折起到 的位置,使二面角
的位置,使二面角 的大小为
的大小为 (如图(4)).
(如图(4)). 的体积;
的体积; 与平面
与平面 所成角的正切值;
所成角的正切值; 为
为 上的点
上的点 ,使
,使 平面
平面


 为任何正数,均有
为任何正数,均有 ;
; .
. 