题目内容
..(本小题满分14分)坐标法是解析几何中最基本的研究方法,坐标法是以坐标系为桥梁,把几何问题转化成代数问题,通过代数运算研究几何图形性质的方法.请利用坐标法解决以下问题:
(Ⅰ)在直角坐标平面内,已知 ,对任意
,对任意 ,试判断
,试判断 的形状;
的形状;
(Ⅱ)在平面内,已知 中,
中, ,
, 为
为 的中点,
的中点, 交
交 于
于 ,求证:
,求证: .
.

(Ⅰ)在直角坐标平面内,已知
 ,对任意
,对任意 ,试判断
,试判断 的形状;
的形状;(Ⅱ)在平面内,已知
 中,
中, ,
, 为
为 的中点,
的中点, 交
交 于
于 ,求证:
,求证: .
.
解:(Ⅰ)解法一: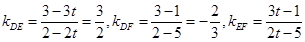 …………3分
…………3分
∴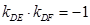 ∴
∴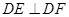
∴ 是直角三角形………………………………………………………6分
是直角三角形………………………………………………………6分
解法二:利用勾股定理(略)
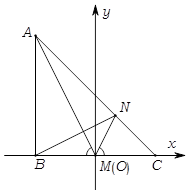
(Ⅱ)解法一:如图,以 为原点,
为原点, 所在直线为
所在直线为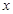 轴建立平面直角坐标系,则
轴建立平面直角坐标系,则
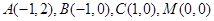 ,
,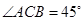 ……………………………8分
……………………………8分
∴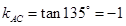 ,直线
,直线 的方程为
的方程为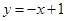 ……………………9分
……………………9分
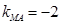 ,直线
,直线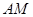 的方程为
的方程为 ,…………………………………10分
,…………………………………10分
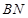 的方程为
的方程为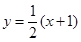 ……………………………………11分
……………………………………11分
联立方程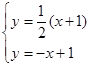 ,解得
,解得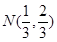 ……………………………12分
……………………………12分
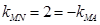 即
即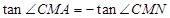 ………………………13分
………………………13分
∴ 又
又
∴ …………………………………………………14分
…………………………………………………14分
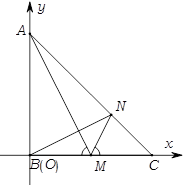
解法二:如图,以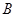 为原点,
为原点, 所在直线为
所在直线为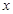 轴建立平面直角坐标系,则
轴建立平面直角坐标系,则
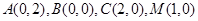 ,
,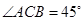 ……………………8分
……………………8分
∴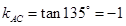 ,直线
,直线 的方程为
的方程为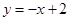 …………………9分
…………………9分
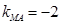 ,直线
,直线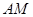 的方程为
的方程为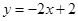 ,…………………………10分
,…………………………10分
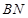 的方程为
的方程为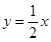 …………………………………………………11分
…………………………………………………11分
联立方程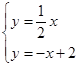 ,解得
,解得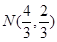 ………………………………12分
………………………………12分
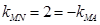 即
即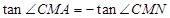 …………………………13分
…………………………13分
∴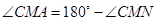
又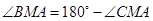
∴ ………………………………………………………14分
………………………………………………………14分
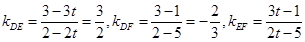 …………3分
…………3分∴
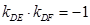 ∴
∴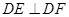
∴
 是直角三角形………………………………………………………6分
是直角三角形………………………………………………………6分解法二:利用勾股定理(略)
(Ⅱ)解法一:如图,以
 为原点,
为原点, 所在直线为
所在直线为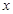 轴建立平面直角坐标系,则
轴建立平面直角坐标系,则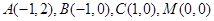 ,
,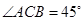 ……………………………8分
……………………………8分∴
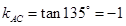 ,直线
,直线 的方程为
的方程为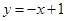 ……………………9分
……………………9分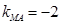 ,直线
,直线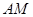 的方程为
的方程为 ,…………………………………10分
,…………………………………10分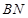 的方程为
的方程为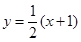 ……………………………………11分
……………………………………11分联立方程
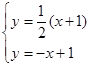 ,解得
,解得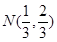 ……………………………12分
……………………………12分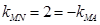 即
即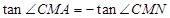 ………………………13分
………………………13分∴
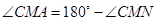 又
又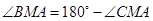
∴
 …………………………………………………14分
…………………………………………………14分

解法二:如图,以
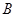 为原点,
为原点, 所在直线为
所在直线为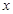 轴建立平面直角坐标系,则
轴建立平面直角坐标系,则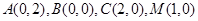 ,
,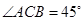 ……………………8分
……………………8分 ∴
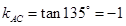 ,直线
,直线 的方程为
的方程为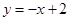 …………………9分
…………………9分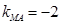 ,直线
,直线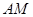 的方程为
的方程为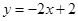 ,…………………………10分
,…………………………10分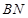 的方程为
的方程为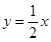 …………………………………………………11分
…………………………………………………11分联立方程
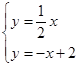 ,解得
,解得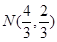 ………………………………12分
………………………………12分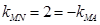 即
即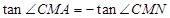 …………………………13分
…………………………13分∴
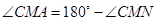
又
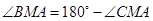
∴
 ………………………………………………………14分
………………………………………………………14分略

练习册系列答案
相关题目




 .
.
 沿对角线
沿对角线 折起,使平面
折起,使平面 平面
平面 ,
, 是
是 的中点,那么异面直线
的中点,那么异面直线 、
、 所成的角的正切值为 。
所成的角的正切值为 。
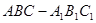 的直观图及三视图(主视图和俯视图是正方形,左侧图是等腰直角三角形)如图,
的直观图及三视图(主视图和俯视图是正方形,左侧图是等腰直角三角形)如图, 为
为 的中点.
的中点. 平面
平面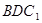 ;
;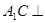 平面
平面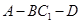 的正切值.
的正切值.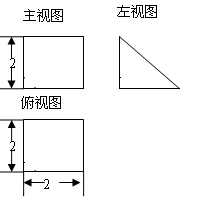
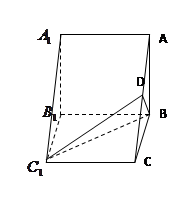
 中,
中, 与
与 所成的角为
所成的角为 ,
, 与
与 所成的角为
所成的角为 ,
, 与
与 ,则有
,则有 



 中,
中, ,
, 为
为 中点,
中点, 为
为 中点,侧面
中点,侧面 为正方形。
为正方形。 平面
平面 ;
; ;
;
 的棱长为1,则与正方体对角线
的棱长为1,则与正方体对角线 垂直的截面面积最大值为
垂直的截面面积最大值为


