题目内容
(12分)如图,在直三棱柱
点D在
(1)证明:无论 为任何正数,均有
为任何正数,均有 ;
;
(2)当 为何值时,二面角
为何值时,二面角 .
.


点D在

(1)证明:无论
 为任何正数,均有
为任何正数,均有 ;
;(2)当
 为何值时,二面角
为何值时,二面角 .
. 
(1)证明:以A为坐标原点建立空间直角坐标系,则

∵ ∴
∴ ,即BD⊥A1C.
,即BD⊥A1C.
(2)解:
设n=(x, y, 1),且n⊥平面A1BD,则
故
即 故
故
设m="(0," 0, 1),则m⊥平面A1B1C1.
∴
又<m, n>与二面角B—A1D—B1相等,即<m, n>=60°,
∴ . ∴当
. ∴当 时,二面角B—A1D—B1="60°. "
时,二面角B—A1D—B1="60°. "

∵
 ∴
∴ ,即BD⊥A1C.
,即BD⊥A1C. (2)解:

设n=(x, y, 1),且n⊥平面A1BD,则

故

即
 故
故
设m="(0," 0, 1),则m⊥平面A1B1C1.
∴

又<m, n>与二面角B—A1D—B1相等,即<m, n>=60°,
∴
 . ∴当
. ∴当 时,二面角B—A1D—B1="60°. "
时,二面角B—A1D—B1="60°. " 略

练习册系列答案
相关题目
 沿对角线
沿对角线 折起,使平面
折起,使平面 平面
平面 ,
, 是
是 的中点,那么异面直线
的中点,那么异面直线 、
、 所成的角的正切值为 。
所成的角的正切值为 。
 的棱长为1,则与正方体对角线
的棱长为1,则与正方体对角线 垂直的截面面积最大值为
垂直的截面面积最大值为








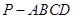 中
中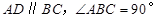 ,
,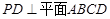 ,
,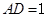 ,
,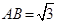 ,
,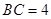 .
.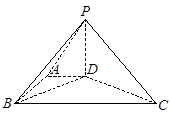
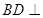
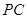 ;
;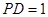 时,求此四棱锥的表面积.
时,求此四棱锥的表面积. 中,异面直线
中,异面直线 与
与 所成角的大小等于
所成角的大小等于 