题目内容
已知矩形 中,
中, ,
, ,点
,点 在
在 上且
上且 (如图(3)).把
(如图(3)).把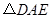 沿
沿 向上折起到
向上折起到 的位置,使二面角
的位置,使二面角 的大小为
的大小为 (如图(4)).
(如图(4)).
(Ⅰ)求四棱锥 的体积;
的体积;
(Ⅱ)求 与平面
与平面 所成角的正切值;
所成角的正切值;
(Ⅲ)设 为
为 的中点,是否存在棱
的中点,是否存在棱 上的点
上的点 ,使
,使 平面
平面 ?若存在,试求出
?若存在,试求出 点位置;若不存在,请说明理由.
点位置;若不存在,请说明理由.

 中,
中, ,
, ,点
,点 在
在 上且
上且 (如图(3)).把
(如图(3)).把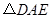 沿
沿 向上折起到
向上折起到 的位置,使二面角
的位置,使二面角 的大小为
的大小为 (如图(4)).
(如图(4)).(Ⅰ)求四棱锥
 的体积;
的体积;(Ⅱ)求
 与平面
与平面 所成角的正切值;
所成角的正切值;(Ⅲ)设
 为
为 的中点,是否存在棱
的中点,是否存在棱 上的点
上的点 ,使
,使 平面
平面 ?若存在,试求出
?若存在,试求出 点位置;若不存在,请说明理由.
点位置;若不存在,请说明理由.
19.解:(1)取AE的中点P,连接DP,
由DA="DE,"

故 为等边三角形,
为等边三角形, 在平面ABCD内的射影H为PD的中点
在平面ABCD内的射影H为PD的中点
 ,又
,又 4分
4分
(2)在三角形CDH中,由
由余弦定理可得
 8分
8分
(3)取CE的中点F,则MF//D/E,在平面ABCE内过F作FN//AE交AB于N,
MF NF=F,D/E
NF=F,D/E AE=E则平面MFN//平面D/AE
AE=E则平面MFN//平面D/AE
又MN在平面MFN内,故MN//平面D/AE
此时AN=EF= CE=
CE= ,故存在N使MN//平面D/AE 12分
,故存在N使MN//平面D/AE 12分

由DA="DE,"


故
 为等边三角形,
为等边三角形, 在平面ABCD内的射影H为PD的中点
在平面ABCD内的射影H为PD的中点 ,又
,又 4分
4分(2)在三角形CDH中,由

由余弦定理可得

 8分
8分(3)取CE的中点F,则MF//D/E,在平面ABCE内过F作FN//AE交AB于N,
MF
 NF=F,D/E
NF=F,D/E AE=E则平面MFN//平面D/AE
AE=E则平面MFN//平面D/AE又MN在平面MFN内,故MN//平面D/AE
此时AN=EF=
 CE=
CE= ,故存在N使MN//平面D/AE 12分
,故存在N使MN//平面D/AE 12分略

练习册系列答案
相关题目
 中,点
中,点 在
在 边上,
边上, ,
, ,
, .
. 的值;
的值; 的面积.
的面积.
 沿对角线
沿对角线 折起,使平面
折起,使平面 平面
平面 ,
, 是
是 的中点,那么异面直线
的中点,那么异面直线 、
、 所成的角的正切值为 。
所成的角的正切值为 。
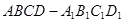 中,
中, 与
与 所成的角为
所成的角为 ,
, 与
与 所成的角为
所成的角为 ,
, 与
与 ,则有
,则有 



 中,
中, ,
, 为
为 中点,
中点, 为
为 中点,侧面
中点,侧面 为正方形。
为正方形。 平面
平面 ;
; ;
;
 为不同的平面,有如下四个命题:其中正确命题的个数是( )
为不同的平面,有如下四个命题:其中正确命题的个数是( ) ②若
②若
 ④若
④若
 的棱长为1,则与正方体对角线
的棱长为1,则与正方体对角线 垂直的截面面积最大值为
垂直的截面面积最大值为



 中,异面直线
中,异面直线 与
与 所成角的大小等于
所成角的大小等于 