题目内容
已知定义在[0,+∞)上的函数f(x)满足f(x)=3f(x+2).当x∈[0,2)时f(x)=-x2+2x.设f(x)在[2n-2,2n)上的最大值为an,且数列{an}的前n项和为Sn,则
Sn= .(其中n∈N*)
| lim |
| n→∞ |
考点:极限及其运算
专题:计算题,函数的性质及应用,等差数列与等比数列
分析:由函数关系式f(x)=3f(x+2),结合f(x)在[2n-2,2n)上的最大值为an可知数列{an}是以
为公比的等比数列,再由当x∈[0,2)时f(x)=-x2+2x求出首项,代入等比数列的前n项和公式求得数列{an}的前n项和为Sn,则其极限可求.
| 1 |
| 3 |
解答:
解:∵定义在[0,+∞)上的函数f(x)满足f(x)=3f(x+2),
∴f(x+2)=
f(x),
就是函数自变量每向右移2个单位,函数值变为原来的
,
∵f(x)在[2n-2,2n)上的最大值为an,且x∈[0,2)时f(x)=-x2+2x,
∴a1=f(1)=1,q=
,
∴数列{an}是以1为首项,以
为公比的等比数列,
则Sn=
=
(1-
).
∴
Sn=
(1-
)=
.
故答案为:
.
∴f(x+2)=
| 1 |
| 3 |
就是函数自变量每向右移2个单位,函数值变为原来的
| 1 |
| 3 |
∵f(x)在[2n-2,2n)上的最大值为an,且x∈[0,2)时f(x)=-x2+2x,
∴a1=f(1)=1,q=
| 1 |
| 3 |
∴数列{an}是以1为首项,以
| 1 |
| 3 |
则Sn=
1×(1-
| ||
1-
|
| 3 |
| 2 |
| 1 |
| 3n |
∴
| lim |
| n→∞ |
| lim |
| n→∞ |
| 3 |
| 2 |
| 1 |
| 3n |
| 3 |
| 2 |
故答案为:
| 3 |
| 2 |
点评:本题考查函数的运算性质,考查了数学转化思想方法,解答此题的关键在于由函数关系式得到数列递推式,考查了数列极限的求法,是中档题.

练习册系列答案
相关题目
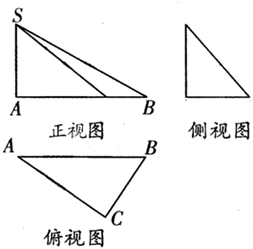 已知三棱锥S-ABC的三视图如图所示,其中俯视图中AC⊥BC,在原三棱锥中给出下列命题:①BC⊥平面SAC;②平面SBC⊥平面SAB;③SB⊥AC.其中所有正确命题是( )
已知三棱锥S-ABC的三视图如图所示,其中俯视图中AC⊥BC,在原三棱锥中给出下列命题:①BC⊥平面SAC;②平面SBC⊥平面SAB;③SB⊥AC.其中所有正确命题是( )| A、①② | B、①③ | C、② | D、① |
设i是虚数单位,则复数z=(
)2013=( )
| 1+i |
| 1-i |
| A、-1 | B、1 | C、-i | D、i |

