题目内容
8．设Sn是等差数列{an}的前n项和，S10=16，S100-S90=24，则S100=200．分析 利用等差数列通项公式列出方程组，求出首项和公差，由此能求出S100．
解答 解：∵Sn是等差数列{an}的前n项和，S10=16，S100-S90=24，
∴$\left\{\begin{array}{l}{10{a}_{1}+\frac{10×9}{2}×d=16}\\{100{a}_{1}+\frac{100×99}{2}d-（90{a}_{1}+\frac{90×89}{2}d）=24}\end{array}\right.$，
解得a1=1.56，$d=\frac{2}{225}$
则S100=100a1+$\frac{100×99}{2}d$=156+$\frac{100×99}{2}×\frac{2}{225}$=200．
故答案为：200．
点评 本题考查等差数列的通项公式的求法，是中档题，解题时要认真审题，注意等差数列的性质的合理运用．
练习册系列答案
阅读快车系列答案
相关题目
16．A、B、C、D、E五位抗战老兵应邀参加了在北京举行的“纪念抗战胜利70周年”大阅兵的老兵方队，现安排这五位老兵分别坐在某辆检阅车的前五排（每两人均不坐同一排），则事件“C坐中间一排，但A与B均不坐第一排”的概率为（ ）
| A． | $\frac{1}{10}$ | B． | $\frac{2}{5}$ | C． | $\frac{3}{20}$ | D． | $\frac{1}{4}$ |
3．
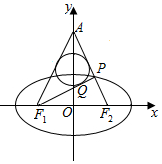如图，焦点在x轴上的椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{3}$=1（a＞0）的左、右焦点分别为F1、F2，P是椭圆上位于第一象限内的一点，且直线F2P与y轴的正半轴交于A点，△APF1的内切圆在边PF1上的切点为Q，若|F1Q|=4，则该椭圆的离心率为（ ）
如图，焦点在x轴上的椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{3}$=1（a＞0）的左、右焦点分别为F1、F2，P是椭圆上位于第一象限内的一点，且直线F2P与y轴的正半轴交于A点，△APF1的内切圆在边PF1上的切点为Q，若|F1Q|=4，则该椭圆的离心率为（ ）| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | $\frac{\sqrt{7}}{4}$ | D． | $\frac{\sqrt{13}}{4}$ |
20．某商业大厦有东南西3个大门，楼内东西两侧各有2个楼梯，从楼外到二楼的不同走法种数是（ ）
| A． | 5 | B． | 7 | C． | 10 | D． | 12 |
17．已知关于x的方程x2-2alnx-2ax=0有唯一解，则实数a的值为（ ）
| A． | 1 | B． | $\frac{1}{2}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{4}$ |