题目内容
19.已知函数f(x),对于实数t,若存在a>0,b>0,满足:?x∈[t-a,t+b],使得|f(x)-f(t)|≤2,则记a+b的最大值为H(t).(1)当f(x)=2x时,H(0)=2;
(2)当f(x)=x2且t∈[1,2]时,函数H(t)的值域为[2$\sqrt{3}$,2$\sqrt{6}$]..
分析 (1)根据题意,当f(x)=2x时,不等式|f(x)-f(0)|≤2化为|2x|≤2,求出解集,得出a+b的最大值H(0);
(2)根据题意,当f(x)=x2且t∈[1,2]时,不等式|f(x)-f(t)|≤2化为|x2-t2|≤2,利用不等式的性质得出x2≤t2+2,求出x的取值范围,得出函数H(t)的值域.
解答 解:(1)根据题意,当f(x)=2x时,存在a>0,b>0,满足:
?x∈[-a,b],使得|f(x)-f(0)|≤2,
即|f(x)|≤2,
∴|2x|≤2,
即|x|≤1,
解得-1≤x≤1;
令$\left\{\begin{array}{l}{-a=-1}\\{b=1}\end{array}\right.$,
解得a=b=1;
∴a+b的最大值为H(0)=2;
(2)根据题意,当f(x)=x2且t∈[1,2]时,
不等式|f(x)-f(t)|≤2可化为|x2-t2|≤2,
∴x2≤t2+2,
即|x|≤$\sqrt{{t}^{2}+2}$;
又t∈[1,2],∴t2∈[1,4],∴t2+2∈[3,6];
∴$\sqrt{{t}^{2}+2}$∈[$\sqrt{3}$,$\sqrt{6}$],
解得-$\sqrt{3}$≤x≤$\sqrt{3}$或-$\sqrt{6}$≤x≤$\sqrt{6}$;
当-$\sqrt{3}$≤x≤$\sqrt{3}$时,H(t)=2$\sqrt{3}$,
当-$\sqrt{6}$≤x≤$\sqrt{6}$时,H(t)=2$\sqrt{6}$;
∴函数H(t)的值域为[2$\sqrt{3}$,2$\sqrt{6}$].
故答案为:(1)2,(2)[2$\sqrt{3}$,2$\sqrt{6}$].
点评 本题考查了新定义函数的性质与应用问题,也考查了不等式的解法与应用问题,是综合性题目.





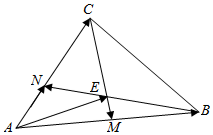 如图所示,在△ABC中,点M为AB的中点,且AN=$\frac{1}{2}$NC,BN与CM相交于点E,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,试以$\overrightarrow{a}$,$\overrightarrow{b}$为基底表示$\overrightarrow{AE}$.
如图所示,在△ABC中,点M为AB的中点,且AN=$\frac{1}{2}$NC,BN与CM相交于点E,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,试以$\overrightarrow{a}$,$\overrightarrow{b}$为基底表示$\overrightarrow{AE}$.