题目内容
3.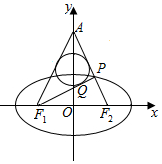 如图,焦点在x轴上的椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{3}$=1(a>0)的左、右焦点分别为F1、F2,P是椭圆上位于第一象限内的一点,且直线F2P与y轴的正半轴交于A点,△APF1的内切圆在边PF1上的切点为Q,若|F1Q|=4,则该椭圆的离心率为( )
如图,焦点在x轴上的椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{3}$=1(a>0)的左、右焦点分别为F1、F2,P是椭圆上位于第一象限内的一点,且直线F2P与y轴的正半轴交于A点,△APF1的内切圆在边PF1上的切点为Q,若|F1Q|=4,则该椭圆的离心率为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{7}}{4}$ | D. | $\frac{\sqrt{13}}{4}$ |
分析 由△APF1的内切圆在边PF1上的切点为Q,根据切线长定理,可得|PQ|=|F1M|-|PF2|,再结合|F1Q|=4,求得|PF1|+|PF2|=8,即a=4,再由隐含条件求得c,则椭圆的离心率可求.
解答 解:如图,△APF1的内切圆在边PF1上的切点为Q
∴根据切线长定理可得|AM|=|AN|,|F1M|=|F1Q|,|PN|=|PQ|
∵|AF1|=|AF2|,
∴|AM|+|F1M|=|AN|+|PN|+|PF2|,
∴|F1M|=|PN|+|PF2|=|PQ|+|PF2|,
∴|PQ|=|F1M|-|PF2|,
则|PF1|+|PF2|=|F1Q|+|PQ|+|PF2|=|F1Q|+|F1M|-|PF2|+|PF2|=2|F1Q|=8,
即2a=8,a=4,
又b2=3,
∴c2=a2-b2=13,则$c=\sqrt{13}$,
∴椭圆的离心率e=$\frac{c}{a}=\frac{\sqrt{13}}{4}$.
故选:D.
点评 本题考查椭圆的离心率,考查三角形内切圆的性质,考查切线长定理,考查学生的计算能力,是中档题.

练习册系列答案
相关题目
12.一个三层书架,分别放置语文书12本,数学书14本,英语书11本,从中取出语文、数学、英语各一本,则不同的取法共有( )
| A. | 37种 | B. | 1848种 | C. | 3种 | D. | 6种 |
13.已知方程x2+(4+i)x+4+ai=0(a∈R)有实根b,且z=a+bi.若复数ω满足|ω-z|≤2,则而|ω|最小值等于( )
| A. | 2$\sqrt{2}$-2 | B. | 2 | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{2}$+2 |
