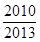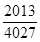题目内容
已知点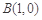 ,
,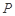 是函数
是函数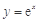 图象上不同于
图象上不同于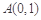 的一点.有如下结论:
的一点.有如下结论:
①存在点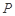 使得
使得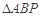 是等腰三角形;
是等腰三角形;
②存在点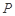 使得
使得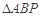 是锐角三角形;
是锐角三角形;
③存在点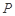 使得
使得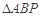 是直角三角形.
是直角三角形.
其中,正确的结论的个数为( )
| A.0 | B.1 | C.2 | D.3 |
B
解析试题分析:∵函数 的导函数为
的导函数为 ,∴
,∴ ,即线段
,即线段 与函数
与函数 图像在
图像在 点的切线垂直,∴
点的切线垂直,∴ 一定是钝角三角形,∴当
一定是钝角三角形,∴当 时,得
时,得 是等腰三角形;故①正确,②③错误,所以正确的结论有1个.
是等腰三角形;故①正确,②③错误,所以正确的结论有1个.
考点:1.函数的导数的应用;2.三角形形状的判定.

练习册系列答案
相关题目
已知函数 有两个极值点,则实数
有两个极值点,则实数 的取值范围是 ( )
的取值范围是 ( )
A. | B. | C. | D. |
已知曲线 的一条切线的斜率为
的一条切线的斜率为 ,则切点的横坐标为( )
,则切点的横坐标为( )
| A.3 | B.2 | C.1 | D. |
定义在R上的函数f(x)满足(x+2) f’(x)<0,又a=f(log0.53),b=f((
f’(x)<0,又a=f(log0.53),b=f((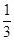 )0.3),c=f(ln3),则( )
)0.3),c=f(ln3),则( )
| A.a<b<c | B.b<c<a | C.c<a<b | D.c< b<a |
定义域为R的连续函数 ,对任意x都有
,对任意x都有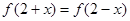 ,且其导函数
,且其导函数 满足
满足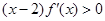 ,则当
,则当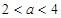 时,有( )
时,有( )
A. | B.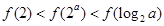 |
C.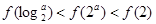 | D.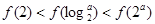 |
设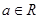 ,函数
,函数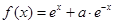 的导函数是
的导函数是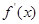 ,且
,且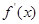 是奇函数。若曲线
是奇函数。若曲线 的一条切线的斜率是
的一条切线的斜率是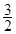 ,则切点的横坐标为( )
,则切点的横坐标为( )
A.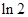 | B.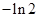 | C.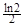 | D.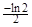 |
已知函数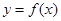 的图像为
的图像为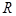 上的一条连续不断的曲线,当
上的一条连续不断的曲线,当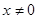 时,
时,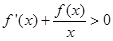 ,则关于
,则关于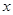 的函数
的函数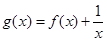 的零点的个数为( )
的零点的个数为( )
| A.0 | B.1 | C.2 | D.0或2 |
设函数f(x)=x3-4x+a,0<a<2.若f(x)的三个零点为x1,x2,x3,且x1<x2<x3,则( )
| A.x1>-1 | B.x2<0 | C.x2>0 | D.x3>2 |
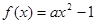 的图像在点A(1,f(1))处的切线l与直线
的图像在点A(1,f(1))处的切线l与直线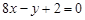 平行,若数列
平行,若数列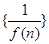 的前
的前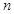 项和为
项和为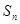 ,则
,则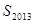 的值为( )
的值为( )