题目内容
设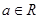 ,函数
,函数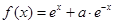 的导函数是
的导函数是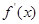 ,且
,且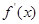 是奇函数。若曲线
是奇函数。若曲线 的一条切线的斜率是
的一条切线的斜率是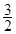 ,则切点的横坐标为( )
,则切点的横坐标为( )
A.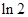 | B.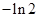 | C.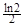 | D.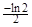 |
A
解析试题分析:由题意可得,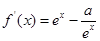 是奇函数,∴
是奇函数,∴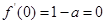 ,∴
,∴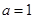 ,
,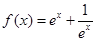 ,
,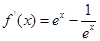 ,∵曲线
,∵曲线 在
在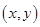 的一条切线的斜率是
的一条切线的斜率是 ,∴
,∴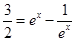 ,解方程可得
,解方程可得 ,∴
,∴ ,故选A.
,故选A.
考点:导数的几何意义.

练习册系列答案
相关题目
设 是定义在R上的可导函数,当x≠0时,
是定义在R上的可导函数,当x≠0时,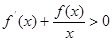 ,则关于x的函数
,则关于x的函数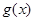
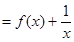 的零点个数为( )
的零点个数为( )
| A.l | B.2 | C.0 | D.0或 2 |
已知曲线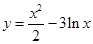 的一条切线的斜率为2,则切点的横坐标为( )
的一条切线的斜率为2,则切点的横坐标为( )
| A.3 | B.2 | C.1 | D. |
已知 为常数,函数
为常数,函数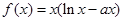 有两个极值点
有两个极值点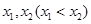 ,则( )
,则( )
A.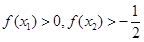 | B.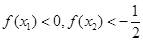 |
C.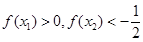 | D.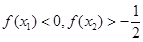 |
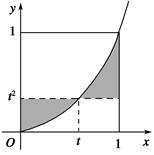
从如图所示的正方形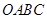 区域内任取一个点
区域内任取一个点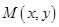 ,则点
,则点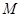 取自阴影部分的概率为( )
取自阴影部分的概率为( )
A.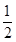 | B.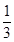 | C.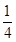 | D.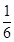 |
下列说法不正确的是( )
A.方程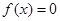 有实数根 有实数根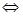 函数 函数 有零点 有零点 |
B.函数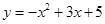 有两个零点 有两个零点 |
| C.单调函数至多有一个零点 |
D.函数 在区间 在区间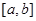 上满足 上满足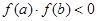 ,则函数 ,则函数 在区间 在区间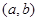 内有零点 内有零点 |
已知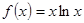 ,若
,若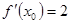 ,则x0等于 ( )
,则x0等于 ( )
A.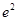 | B.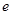 | C. | D. |
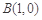 ,
,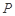 是函数
是函数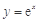 图象上不同于
图象上不同于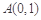 的一点.有如下结论:
的一点.有如下结论: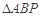 是等腰三角形;
是等腰三角形;