题目内容

【题目】已知数列中， ， .

（Ⅰ）证明数列是等比数列；

（Ⅱ）若是数列的前项和，求.

【答案】(Ⅰ)证明见解析；(Ⅱ) .

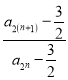【解析】试题分析：本题主要考查等比数列的证明、等差数列和等比数列的前n项和公式等基础知识，考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问，利用来证明数列为等比数列，所以，然后将分段函数代入，直到代入化简，得常数，即可证明数列为等比数列；第二问，利用第一问的结论得到等比数列的通项公式，从而得到的通项公式，再利用分段函数得到的通项公式，再利用分组求和的方法求的值.

试题解析：（1）设，则， 2分

因为

所以数列是以为首项， 为公比的等比数列. 6分

（2）由（1）得，

即， 8分

由，

得， 10分

所以，

， 12分

练习册系列答案
相关题目

【题目】如图，在四棱锥PABCD中，PA⊥平面ABCD，AD∥BC，AD⊥CD，且AD＝CD＝2，BC＝4，PA＝2.

(1)求证：AB⊥PC；

(2)在线段PD上，是否存在一点M，使得二面角MACD的大小为45°，如果存在，求BM与平面MAC所成角的正弦值，如果不存在，请说明理由．

【题目】已知中心在坐标原点，一个焦点为的椭圆被直线截得的弦的中点的横坐标为.

（1）求此椭圆的方程；

（2）设直线与椭圆交于两点，且以为对角线的菱形的一个顶点为，求面积的最大值及此时直线的方程.

【题目】如果的定义域为，对于定义域内的任意，存在实数使得成立，则称此函数具有“性质”.给出下列命题：

①函数具有“性质”；

②若奇函数具有“性质”，且，则；

③若函数具有“性质”，图象关于点成中心对称，且在上单调递减，则在上单调递减，在上单调递增；

④若不恒为零的函数同时具有“性质”和“性质”，且函数对，都有 成立，则函数是周期函数.

其中正确的是__________（写出所有正确命题的编号）．

【题目】在某校组织的高二女子排球比赛中，有、两个球队进入决赛，决赛采用7局4胜制．假设、两队在每场比赛中获胜的概率都是．并记需要比赛的场数为．

（Ⅰ）求大于4的概率；

（Ⅱ）求的分布列与数学期望．

【题目】已知函数f(x)＝x＋1＋|3－x|，x≥－1.

(1)求不等式f(x)≤6的解集；

(2)若f(x)的最小值为n，正数a，b满足2nab＝a＋2b，求2a＋b的最小值．

【题目】已知函数为偶函数，且函数

图象的两相邻对称轴间的距离为.

（1）求的值；

（2）将函数的图象向右平移个单位后，再将得到的图象上各点的横坐标伸长到原来的倍，纵坐标不变，得到函数的图象，求的单调递减区间.

【题目】如图所示，在几何体中，四边形是菱形，平面，，且，.

(1)证明：平面平面；

(2)若二面角是直二面角，求异面直线与所成角的余弦值．

【题目】已知函数 ， ．

（Ⅰ）当 时， 恒成立，求的取值范围；

（Ⅱ）当 时，研究函数的零点个数；

（Ⅲ）求证： (参考数据： )．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网