题目内容
16.在下列各图中y=kx+b(k≠0)与y=kx2+bx的图象可能是( )| A. | 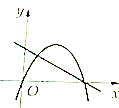 | B. | 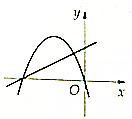 | C. | 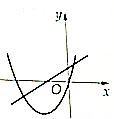 | D. | 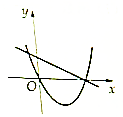 |
分析 由直线确定k、b的符号,从而得到y=kx2+bx的开口方向及零点,结合图形,得出结论.
解答 解:对于选项A,由直线y=kx+b,可得k<0,b>0,
∴二次函数的图象开口向下,且图象的对称轴为x=-$\frac{b}{2k}$>0,
二次函数的零点为0,-$\frac{b}{k}$,故满足条件.
对于选项B,由直线y=kx+b,可得k>0,b>0,
∴二次函数的图象开口向上,故不满足条件.
对于选项C,由直线y=kx+b,可得k>0,b>0,故直线和x轴的交点为(-$\frac{b}{k}$,0).
∴二次函数y=kx2+bx=x(kx+b)的图象开口向上,二次函数的零点为0,-$\frac{b}{k}$,
而由图象可得抛物线的零点和直线的零点不重合,故选项C不满足条件.
对于选项D,由直线y=kx+b,可得k<0,b>0,
∴二次函数的图象开口向下,故满足条件.
故选:A.
点评 本题考查了同一坐标系一次函数图象与二次函数图象的关系,根据指数函数图象确定出a、b的正负情况是求解的关键,属于中档题.

练习册系列答案
相关题目
7.若集合$A=\{x|\frac{x+5}{x-2}<0\}$,B={x|-4<x<3},则集合A∩B为( )
| A. | {x|-5<x<3} | B. | {x|-4<x<2} | C. | {x|-4<x<5} | D. | {x|-2<x<3} |
11.执行如图所示的程序框图,输出的i为( )


| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
5.已知数列{an}的前n项和Sn=2n2-3n,而a1,a3,a5,a7,…组成一新数列{Cn},其通项公式为( )
| A. | Cn=4n-3 | B. | Cn=8n-1 | C. | Cn=4n-5 | D. | Cn=8n-9 |
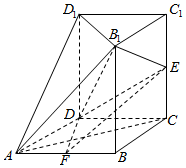 如图,几何体ABCD-B1C1D1中,四边形ABCD为菱形,∠BAD=60°,AB=a,平面B1C1D1∥平面ABCD,BB1、CC1、DD1都垂直于平面ABCD,且BB1=$\sqrt{2}$a,E为CC1的中点,F为AB的中点.
如图,几何体ABCD-B1C1D1中,四边形ABCD为菱形,∠BAD=60°,AB=a,平面B1C1D1∥平面ABCD,BB1、CC1、DD1都垂直于平面ABCD,且BB1=$\sqrt{2}$a,E为CC1的中点,F为AB的中点.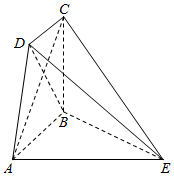 如图,五面体ABCDE中,AB∥CD,CB⊥平面ABE,AE⊥AB,AB=AE=2,BC=$\sqrt{2}$,CD=1.
如图,五面体ABCDE中,AB∥CD,CB⊥平面ABE,AE⊥AB,AB=AE=2,BC=$\sqrt{2}$,CD=1.