题目内容
5.已知数列{an}的前n项和Sn=2n2-3n,而a1,a3,a5,a7,…组成一新数列{Cn},其通项公式为( )| A. | Cn=4n-3 | B. | Cn=8n-1 | C. | Cn=4n-5 | D. | Cn=8n-9 |
分析 由数列{an}的前n项和Sn=2n2-3n,得到an=Sn-Sn-1可求得数列{an}的通项公式.
解答 解:∵Sn=2n2-3n,
∴当n≥2时,
an=Sn-Sn-1
=2n2-3n-[2(n-1)2-3(n-1)]
=4n-5,
当n=1时,a1=S1=-1也符合上式,
∴an=4n-5.
故选:C.
点评 本题考查数列的求和,着重考查等差数列的通项公式,属于基础题.

练习册系列答案
相关题目
15.用1,2,3,4,5五个数字可排成没有重复数字,且大于20000,又不是5的倍数的五位数有( )
| A. | 96个 | B. | 78个 | C. | 72个 | D. | 36个 |
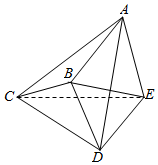 在如图所示的几何体ABCDE中,AE⊥平面DCE,BE=$\sqrt{6}$,DC=4,BD=2,CE=2$\sqrt{3}$,∠BCD=30°,CE⊥AD.
在如图所示的几何体ABCDE中,AE⊥平面DCE,BE=$\sqrt{6}$,DC=4,BD=2,CE=2$\sqrt{3}$,∠BCD=30°,CE⊥AD.