题目内容
16.函数f(x)=$\frac{1}{{\sqrt{-{x^2}+2x+3}}}+ln({x^2}-1)$ 的定义域是{x|1<x<3}.分析 根据二次根式的性质以及对数函数的性质求出函数的定义域即可.
解答 解:由题意得:
$\left\{\begin{array}{l}{{-x}^{2}+2x+3>0}\\{{x}^{2}-1>0}\end{array}\right.$,
解得:1<x<3,
故答案为:{x|1<x<3}.
点评 本题考查了求函数的定义域问题,考查对数函数以及二次根式的性质,是一道基础题.

练习册系列答案
相关题目
7.要得到函数$y=\frac{{\sqrt{2}}}{2}sinx+\frac{{\sqrt{2}}}{2}cosx+1$的图象,需要把函数y=sinx的图象( )
| A. | 向右平移$\frac{π}{4}$个单位,再向上平移1个单位 | |
| B. | 向左平移$\frac{π}{4}$个单位,再向上平移1个单位 | |
| C. | 向左平移$\frac{π}{4}$个单位,再向下平移1个单位 | |
| D. | 向右平移$\frac{π}{4}$个单位,再向下平移1个单位 |
4.已知sinα+cosα=-$\frac{1}{5}$,α∈(0,π),则tanα的值为( )
| A. | -$\frac{4}{3}$或-$\frac{3}{4}$ | B. | -$\frac{4}{3}$ | C. | -$\frac{3}{4}$ | D. | $\frac{3}{4}$ |
8.满足{1,2}?A⊆{1,2,3,4,5,6}的集合A的个数有( )个.
| A. | 13 | B. | 14 | C. | 15 | D. | 16 |
6.点P(1,-1)到直线ax+3y+2a-6=0的距离的最大值为( )
| A. | $2\sqrt{2}$ | B. | $2\sqrt{3}$ | C. | $3\sqrt{2}$ | D. | $3\sqrt{3}$ |
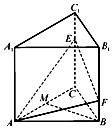 三棱柱ABC-A1B1C1的底面是边长为2的正三角形,侧棱A1A⊥底面ABC,点E,F分别是棱CC1,BB1上的点,点M是线段AC上的动点,EC=2FB=2.
三棱柱ABC-A1B1C1的底面是边长为2的正三角形,侧棱A1A⊥底面ABC,点E,F分别是棱CC1,BB1上的点,点M是线段AC上的动点,EC=2FB=2.