题目内容
在等差数列{an}中，a30+a70=200，则S99的值为（ ）
| A、9900 | B、10000 |
| C、100 | D、4950 |
考点：等差数列的前n项和
专题：等差数列与等比数列
分析：利用等差数列的通项公式和前n项和公式求解．
解答：
解：∵在等差数列{an}中，a30+a70=200，
S99=
(a1+a99)=
(a30+a70)=
×200=9900．
故选：A．
S99=
| 99 |
| 2 |
| 99 |
| 2 |
| 99 |
| 2 |
故选：A．
点评：本题考查等差数列的前99项和的求法，解题时要认真审题，注意等差数列的性质的合理运用．
练习册系列答案
相关题目
从一堆苹果中任取了20个，并得到它们的质量（单位：克）数据分布表如下：
则这堆苹果中，质量不小于120克的苹果数约占苹果总数的（ ）
| 分组 | [90，100） | [100，110） | [110，120） | [120，130） | [130，140） | [140，150] |
| 频数 | 1 | 2 | 3 | 10 | 3 | 1 |
| A、30% | B、70% |
| C、60% | D、50% |
已知等差数列{an}中a3+a9+a15=9，则数列{an}的前17项和S17=（ ）
| A、102 | B、36 | C、48 | D、51 |
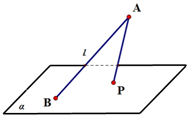如图，点A是平面α外一定点，过A作平面α的斜线l，斜线l与平面α所成角为50°．若点P在平面α内运动，并使直线AP与l所成角为35°，则动点P的轨迹是（ ）| A、圆 | B、椭圆 |
| C、抛物线 | D、双曲线的一支 |
已知函数f（x）=
sin（
x），为了得到函数g（x）=sin（
x）+cos（
x）的图象，只要将y=f（x）的图象（ ）
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
A、向右平移
| ||
B、向左平移
| ||
C、向右平移
| ||
D、向左平移
|