题目内容
11.设函数f(x)=$\sqrt{3}$sin(ωx+φ)+cos(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的最小正周期为2π,且其图象关于y轴对称,则( )| A. | f(x)在(0,$\frac{π}{2}$)上单调递增 | B. | f(x)在($\frac{π}{4}$,$\frac{3π}{2}$)上单调递减 | ||
| C. | f(x)在(0,$\frac{π}{2}$)上单调递减 | D. | f(x)在($\frac{π}{4}$,$\frac{3π}{2}$)上单调递增 |
分析 由辅助角公式将f(x)=2sin(ωx+φ+$\frac{π}{6}$),由最小正周期2π,ω=1,关于y为对称轴,求得φ,利用余弦函数图象即可求得答案.
解答 解:f(x)=$\sqrt{3}$sin(ωx+φ)+cos(ωx+φ)=2sin(ωx+φ+$\frac{π}{6}$),
最小正周期T=$\frac{2π}{ω}$=2π,
∴ω=1,
∵图象关于y轴对称,
∴φ+$\frac{π}{6}$=kπ+$\frac{π}{2}$,
∴φ=$\frac{π}{3}$,
∴f(x)=2cosx,
由函数图象可知: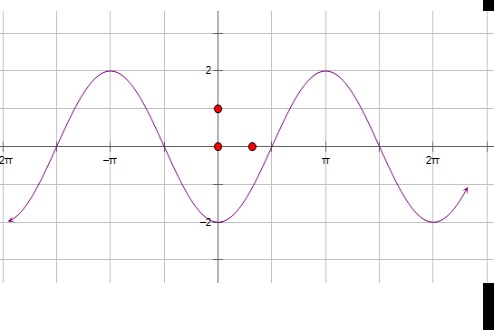
∴故答案:C.
点评 本题考查三角恒等变换及函数图象,根据函数图象求函数的单调性,属于基础题.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
4.设偶函数f(x)的定义域为R,当x∈[0,+∞)时函数f(x)是减函数,则f(-3),f(π),f(-3.14)的大小关系为( )
| A. | f(π)=f(-3.14)>f(-3) | B. | f(π)<f(-3.14)<f(-3) | C. | f(π)>f(-3.14)>f(-3) | D. | f(π)<f(-3)<f(-3.14) |
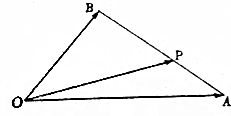 如图,在△OAB中,已知P为线段AB上的一点.|$\overrightarrow{OA}$|=4,|$\overrightarrow{OB}$|=3,且$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为60°.
如图,在△OAB中,已知P为线段AB上的一点.|$\overrightarrow{OA}$|=4,|$\overrightarrow{OB}$|=3,且$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为60°.