题目内容
17.已知f(x)=sin(2x+$\frac{π}{6}$),x∈R.(1)求函数f(x)的最小正周期.
(2)单调递增区间.
(3)用“五点作图”画出它某一周期的图象.
分析 (1)利用三角函数周期公式即可计算得解.
(2)由2kπ-$\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,k∈Z,即可解得函数的单调递增区间.
(3)用五点法作函数y=Asin(ωx+φ)的图象即可得解.
解答 解:(1)∵f(x)=sin(2x+$\frac{π}{6}$),x∈R.
∴函数f(x)的最小正周期T=$\frac{2π}{2}$=π.
(2)由2kπ-$\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,k∈Z,解得:kπ-$\frac{π}{3}$≤x≤kπ+$\frac{π}{6}$,k∈Z,
可得函数f(x)的单调递增区间为:[kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$],k∈Z,
(3)∵函数f(x)=sin(2x+$\frac{π}{6}$),列表可得:
| 2x+$\frac{π}{6}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | -$\frac{π}{12}$ | $\frac{π}{6}$ | $\frac{5π}{12}$ | $\frac{2π}{3}$ | $\frac{11π}{12}$ |
| f(x) | 0 | 1 | 0 | -1 | 0 |

点评 本题主要考查了用五点法作函数y=Asin(ωx+φ)在一个周期上的简图,考查了正弦函数的单调性、周期性的应用,属于中档题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
7.复数z=$\frac{m-2i}{1-2i}$(m∈R)不可能在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
8.设等差数列{an}的前n项和为Sn,若S4=8,S8=20,则a9+a10+a11+a12=( )
| A. | 18 | B. | 17 | C. | 16 | D. | 15 |
12.过点p(1,2)且与直线3x+y-1=0平行的直线方程是( )
| A. | 3x+y-5=0 | B. | x+3y-7=0 | C. | x-3y+5=0 | D. | x-3y-5=0 |
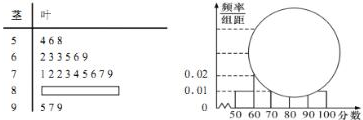 某校高一某班的一次数学测试成绩(满分为100分)的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如图,据此解答如下问题;
某校高一某班的一次数学测试成绩(满分为100分)的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如图,据此解答如下问题;