题目内容
10.设A、B是钝角三角形的两个锐角,则点P(sinA-cosB,cosA-sinB)在( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 由题意知A、B、是锐角,C是钝角,推出A、B的关系,分别求它的正弦和余弦,即可得到结果.
解答 解:在钝角三角形ABC中,A<90°,B<90°,C>90°,
又因为A+B+C=180°,则A+B<90°,
∴A<90°-B.
又因为y=cosx在0°<x<90°上单调减,即cosx的值随x的增加而减少,
∴cosA>cos(90°-B)=sinB,
即cosA>sinB,cosA-sinB>0
同理B<90°-A,则cosB>cos(90°-A)=sinA,
∴sinA-cosB>0
故点P在第四象限.
故选:D.
点评 本题考查三角形的内角和定理,正弦函数与余弦函数的性质,诱导公式,三角函数线的应用,考查转化思想,属于中档题.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
19.已知向量$\overrightarrow a=({-2,2})$,$\overrightarrow b=({5,m})$,且|$\overrightarrow a+\overrightarrow b|$不超过5,则函数f(x)=$\sqrt{3}$cosx-sinx+m有零点的概率是( )
| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{1}{2}$ |
20.数列-$\frac{1}{2}$,$\frac{1}{4}$,-$\frac{1}{8}$,$\frac{1}{16}$,…的一个通项公式是( )
| A. | -$\frac{1}{{2}^{n}}$$\frac{(-1)^{n}}{{2}^{n}}$ | B. | $\frac{(-1)^{n}}{{2}^{n}}$ | C. | $\frac{(-1)^{n+1}}{{2}^{n}}$ | D. | $\frac{(-1)^{n}}{{2}^{n-1}}$ |
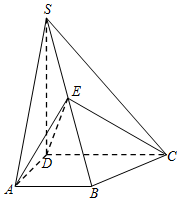 如图,在四棱锥S-ABCD中,已知SD⊥底面ABCD,且四边形ABCD为直角梯形,∠DAB=∠ADC=$\frac{π}{2}$,SD=DC=2,AD=AB=1,E为棱SB上的一点,且DE⊥SC.
如图,在四棱锥S-ABCD中,已知SD⊥底面ABCD,且四边形ABCD为直角梯形,∠DAB=∠ADC=$\frac{π}{2}$,SD=DC=2,AD=AB=1,E为棱SB上的一点,且DE⊥SC.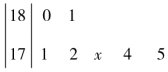 某校文科班7名男生身高(单位:厘米)分布的茎叶图如图,已知7名男生的平均身高为175cm,但有一名男生的身高不清楚,只知道其末位数为x,那么x的值为2.
某校文科班7名男生身高(单位:厘米)分布的茎叶图如图,已知7名男生的平均身高为175cm,但有一名男生的身高不清楚,只知道其末位数为x,那么x的值为2.