题目内容
9.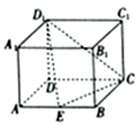 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E为AB的中点,则点B到平面D1EC的距离为$\frac{\sqrt{2}}{2}$.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E为AB的中点,则点B到平面D1EC的距离为$\frac{\sqrt{2}}{2}$.
分析 以D为原点,建立空间直角坐标系,利用向量法能求出点B到平面D1EC的距离.
解答 解: ∵在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,
∵在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,
点E为AB的中点,
以D为原点,建立空间直角坐标系,如图
∴B(1,2,0),C(0,2,0)E(1,1,0),
D1(0,0,1),
$\overrightarrow{EB}$=(0,1,0),$\overrightarrow{EC}$=(-1,1,0),
$\overrightarrow{E{D}_{1}}$=(-1,-1,1),
设平面D1EC的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{EB}=y=0}\\{\overrightarrow{n}•\overrightarrow{E{D}_{1}}=-x-y+z=0}\end{array}\right.$,
取y=1,得$\overrightarrow{n}$=(0,1,1),
∴点B到平面D1EC的距离:
d=$\frac{|\overrightarrow{EB}•\overrightarrow{n}|}{|\overrightarrow{n}|}$=$\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}$.
故答案为:$\frac{\sqrt{2}}{2}$.
点评 本题考查点到平面的距离的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.已知命题p:?x∈R,x2-x+1≤0,则( )
| A. | ¬p:?x0∈R,x02-x0+1≤0 | B. | ¬p:?x∈R,x2-x+1≥0 | ||
| C. | ¬p:?x∈R,x2-x+1>0 | D. | ¬p:?0x∈R,x02-x0+1>0 |
4.已知空间向量$\overrightarrow{a}$=(0,$\frac{5}{4}$,-$\frac{5}{4}$),$\overrightarrow{b}$=(x,0,-2),则“x=2”是“<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{π}{3}$”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
14.抛物线y=9x2的焦点坐标为( )
| A. | ($\frac{1}{36}$,0) | B. | (0,$\frac{1}{36}$) | C. | ($\frac{9}{4}$,0) | D. | (0,$\frac{9}{4}$) |