题目内容
20.若sinx+cosx=$\sqrt{2}$,则tanx=1.分析 将已知等式两边平方可得2sinxcosx=1,化为$\frac{2sinxcosx}{si{n}^{2}x+co{s}^{2}x}$=1,利用同角三角函数基本关系式可得:$\frac{2tanx}{ta{n}^{2}x+1}$=1,整理即可解得tanx的值.
解答 解:∵sinx+cosx=$\sqrt{2}$,
∴两边平方可得:1+2sinxcosx=2,解得:2sinxcosx=1,
∴$\frac{2sinxcosx}{si{n}^{2}x+co{s}^{2}x}$=1,可得:$\frac{2tanx}{ta{n}^{2}x+1}$=1,整理可得:tan2x-2tanx+1=0,
∴解得:tanx=1.
故答案为:1.
点评 本题主要考查了同角三角函数基本关系式在三角函数化简求值中的应用,考查了转化思想,属于基础题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
11.已知直线y=x+1与曲线y=f(x)=ln(x+a)相切,则${∫}_{1}^{2}$f′(x-2)dx=( )
| A. | 1 | B. | ln2 | C. | 2ln2 | D. | 2 |
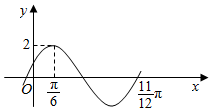 函数f(x)=2sin(ωx+φ)(ω>0,0<φ<π)的部分图象如图所示.
函数f(x)=2sin(ωx+φ)(ω>0,0<φ<π)的部分图象如图所示.