题目内容
19.已知函数f(x)=sinωx-2$\sqrt{3}$sin2$\frac{ωx}{2}$+$\sqrt{3}$(ω>0),其图象与x轴的相邻两个交点的距离为$\frac{π}{2}$,则f(x)在区间[0,$\frac{π}{2}$]上的最小值为( )| A. | -2 | B. | 2 | C. | -$\sqrt{3}$ | D. | -2$\sqrt{3}$ |
分析 化简已知函数可得f(x)=2sin(2ωx+$\frac{π}{3}$),由图象和周期性可得ω值,由x的范围和三角函数最值可得.
解答 解:由三角函数公式可得f(x)=sinωx-2$\sqrt{3}$sin2$\frac{ωx}{2}$+$\sqrt{3}$
=sinωx+$\sqrt{3}$(1-2sin2$\frac{ωx}{2}$)=sinωx+$\sqrt{3}$cos2ωx
=2sin(2ωx+$\frac{π}{3}$),
∵图象与x轴的相邻两个交点的距离为$\frac{π}{2}$,
∴函数的周期T=π=$\frac{2π}{2ω}$,解得ω=1,
∴f(x)=2sin(2x+$\frac{π}{3}$),
∵x∈[0,$\frac{π}{2}$],∴2x+$\frac{π}{3}$∈[$\frac{π}{3}$,$\frac{4π}{3}$],
∴sin(2x+$\frac{π}{3}$)∈[-$\frac{\sqrt{3}}{2}$,1],
∴2sin(2x+$\frac{π}{3}$)∈[-$\sqrt{3}$,2],
∴f(x)在区间[0,$\frac{π}{2}$]上的最小值为-$\sqrt{3}$,
故选:C.
点评 本题考查三角函数恒等变换,涉及三角函数的周期性和最值,属中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
10.一个蜂巢里有1只蜜蜂,第一天它飞出去找回3个伙伴;第2天有4只蜜蜂飞出去各自找回了3个伙伴,…,如果这个找伙伴的过程继续下去,第6天所有的蜜蜂归巢后,蜂巢中一共有( )只蜜蜂.
| A. | 972 | B. | 1456 | C. | 4096 | D. | 5460 |
 在如图所示的直三棱柱ABC-A1B1C1,AC=1,BC=$\sqrt{2}$,AB=$\sqrt{3}$,侧棱AA1=1,点D,M分别为A1B,B1C1的中点.
在如图所示的直三棱柱ABC-A1B1C1,AC=1,BC=$\sqrt{2}$,AB=$\sqrt{3}$,侧棱AA1=1,点D,M分别为A1B,B1C1的中点.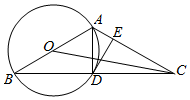 如图,以△ABC的边AB为直径作⊙O,⊙O与边BC的交点D恰为BC边的中点,过点D作DE⊥AC于点E.
如图,以△ABC的边AB为直径作⊙O,⊙O与边BC的交点D恰为BC边的中点,过点D作DE⊥AC于点E.