题目内容
8．设变量x，y满足约束条件$\left\{\begin{array}{l}{x+3y-3≤0}\\{x-y+1≥0}\\{y≥-1}\end{array}\right.$，则z=2x+y+1的最大值为12．分析 作出不等式组对应的平面区域，利用目标函数的几何意义，即可求最大值．
解答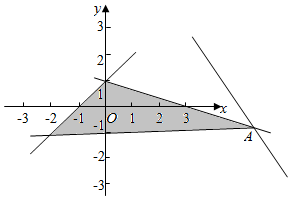 
解：作出不等式组$\left\{\begin{array}{l}{x+3y-3≤0}\\{x-y+1≥0}\\{y≥-1}\end{array}\right.$，对应的平面区域如图：（阴影部分）
由z=2x+y+1得y=-2x+z-1，
平移直线y=-2x+z-1，
由图象可知当直线y=-2x+z-1经过点A时，直线y=-2x+z-1的截距最大，
此时z最大．
由$\left\{\begin{array}{l}{y=-1}\\{x+3y-3=0}\end{array}\right.$，解得：$\left\{\begin{array}{l}{x=6}\\{y=-1}\end{array}\right.$，即A（6，-1），
代入目标函数z=2x+y+1得z=2×6-1+1=12．
即目标函数z=2x+y+1的最大值为12．
故答案为：12．
点评 本题主要考查线性规划的应用，利用目标函数的几何意义，结合数形结合的数学思想是解决此类问题的基本方法．
练习册系列答案
相关题目
4．一群人中，37.5%的人为A型血，20.9%的人为B型血，33.7%的人为O型血，7.9%的人为AB型血，已知能允许输血的血型配对如下表，现在这群人中任选1人为输血者，再选1人为受血者，问：输血能成功的概率是多少？（注：“+”表示允许输血，“/”表示不允许输血）
| 输血者/受血者 | A型 | B型 | AB型 | O型 |
| A型 | + | / | / | + |
| B型 | / | + | / | + |
| AB型 | + | + | + | + |
| O型 | / | / | / | + |
19．已知函数f（x）=sinωx-2$\sqrt{3}$sin2$\frac{ωx}{2}$+$\sqrt{3}$（ω＞0），其图象与x轴的相邻两个交点的距离为$\frac{π}{2}$，则f（x）在区间[0，$\frac{π}{2}$]上的最小值为（ ）
| A． | -2 | B． | 2 | C． | -$\sqrt{3}$ | D． | -2$\sqrt{3}$ |
13．已知平面向量$\overrightarrow{a}$=（-$\sqrt{3}$，m），$\overrightarrow{b}$=（2，1）且$\overrightarrow{a}$⊥$\overrightarrow{b}$，则实数m的值为（ ）
| A． | $-2\sqrt{3}$ | B． | $2\sqrt{3}$ | C． | $4\sqrt{3}$ | D． | $6\sqrt{3}$ |
20．已知全集U=R，集合A={x|lgx≥0}，$B=\left\{{x\left|{{2^x}≥\sqrt{2}}\right.}\right\}$，则A∩B为（ ）
| A． | {x|x≥1} | B． | $\left\{{x\left|{x≥\frac{1}{2}}\right.}\right\}$ | C． | {x|0＜x≤1} | D． | $\left\{{x\left|{0＜x≤\frac{1}{2}}\right.}\right\}$ |
18．已知函数f（x）=sin（2ωx+$\frac{π}{3}$）（ω＞0）下的最小正周期为π，则函数的图象（ ）
| A． | 关于直线x=$\frac{13π}{12}$对称 | B． | 关于点（-$\frac{π}{12}$，0）对称 | ||
| C． | 关于直线x=-$\frac{7π}{12}$对称 | D． | 关于点（$\frac{π}{4}$，0）对称 |