题目内容
定义在R上的函数f(x)满足f(4)=1.f ′(x)为f(x)的导函数,已知函数y=f ′(x)的图象如图所示.若两正数a,b满足f(2a+b)<1,则的取值范围是( )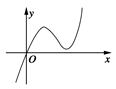
A.( , , ) ) |
B.(-∞, )∪(3,+∞) )∪(3,+∞) |
C.( ,3) ,3) |
| D.(-∞,-3) |
C
解析试题分析:由 的图象知,当
的图象知,当 时,
时, ,函数
,函数 是减函数;当
是减函数;当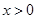 时,
时, ,函数f(x)是增函数;两正数
,函数f(x)是增函数;两正数 满足
满足 ,点
,点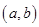 的区域为图中的阴影部分(不包括边界),
的区域为图中的阴影部分(不包括边界), 的意义为阴影部分的点与点
的意义为阴影部分的点与点 连线的斜率,直线
连线的斜率,直线 的斜率分别为
的斜率分别为 ,则
,则 的取值范围是
的取值范围是 ,故选C.
,故选C.
考点:1、导数与函数的单调性;2、二元一次不等式组所表示的平面区域;3、数形结合的思想.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
 的值是( ).
的值是( ).
A. | B. | C. | D. |
函数f(x)的定义域为R,f(-1)=2,对任意x∈R,f′(x)>2,则f(x)>2x+4的解集为( )
| A.(-1,1) | B.(-1,+∞) |
| C.(-∞,-1) | D.(-∞,+∞) |
已知函数f(x)=cosxsin2x,下列结论中错误的是( )
| A.y=f(x)的图像关于点(π,0)中心对称 |
B.y=f(x)的图像关于直线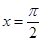 对称 对称 |
C.f(x)的最大值为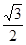 |
| D.f(x)既是奇函数,又是周期函数 |
已知α∈R, ,则tan2α=( )
,则tan2α=( )
A. | B. | C. | D. |
 的结果为
的结果为  ,在区间
,在区间 上恰有一个零点,解不等式
上恰有一个零点,解不等式 .
. 在
在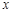 = 处取得极小值.
= 处取得极小值. ,且与曲线
,且与曲线 相切,则直线
相切,则直线 的方程为 .
的方程为 .