题目内容
函数f(x)的定义域为R,f(-1)=2,对任意x∈R,f′(x)>2,则f(x)>2x+4的解集为( )
| A.(-1,1) | B.(-1,+∞) |
| C.(-∞,-1) | D.(-∞,+∞) |
B
解析试题分析:依题意可设 ,所以
,所以 .所以函数
.所以函数 在R上单调递增又因为
在R上单调递增又因为 .所以要使
.所以要使 ,只需要
,只需要 .故选B.
.故选B.
考点:1.函数的求导.2.函数的单调性.3构建新的函数的思想.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
定义在R上的函数f(x)满足f(4)=1.f ′(x)为f(x)的导函数,已知函数y=f ′(x)的图象如图所示.若两正数a,b满足f(2a+b)<1,则的取值范围是( )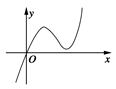
A.( , , ) ) |
B.(-∞, )∪(3,+∞) )∪(3,+∞) |
C.( ,3) ,3) |
| D.(-∞,-3) |
设 的图象是将函数
的图象是将函数 向左平移
向左平移 个单位得到的,则
个单位得到的,则 等于( )
等于( )
| A.1 | B.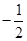 | C.0 | D. |
 ,使
,使 ”的否定是“
”的否定是“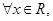 使
使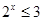 ”;
”;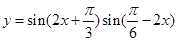 的最小正周期是
的最小正周期是 ;
;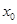 处有极值,则
处有极值,则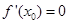 ”的否命题是真命题;
”的否命题是真命题;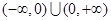 上的奇函数,x>0时的解析式是
上的奇函数,x>0时的解析式是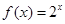 ,则x<0时的解析式为
,则x<0时的解析式为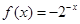 .
. ,则
,则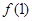 的值为 .
的值为 . ;(2)
;(2)
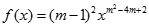 在
在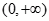 上单调递增,函数
上单调递增,函数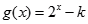 .
.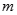 的值;
的值;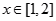 时,记
时,记 ,
,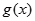 的值域分别为集合
的值域分别为集合 ,若
,若 ,求实数
,求实数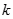 的取值范围.
的取值范围.
 = .
= . (
(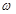 >0,︱
>0,︱ ︱<
︱< )的部分图像如图,则
)的部分图像如图,则