题目内容
6.(1)已知全集U=R,集合A={x|1≤x-1<3},B={x|2x-9≥6-3x}.求:(1)①A∪B; ②∁U(A∩B)
(2)化简:(-2x${\;}^{\frac{1}{4}}$y${\;}^{-\frac{1}{3}}$)(3x${\;}^{-\frac{1}{2}}$y${\;}^{\frac{2}{3}}$)(-4x${\;}^{\frac{1}{4}}$y${\;}^{\frac{2}{3}}$).
分析 (1)根据集合的基本运算进行求解,
(2)根据指数幂的运算法则进行化简即可.
解答 解:(1)A={x|1≤x-1<3}={x|2≤x<4},B={x|2x-9≥6-3x}={x|x≥3}.
则A∪B{x|x≥2},A∩B={x|3≤x<4},
则∁U(A∩B)={x|x<3或x≥4}.
(2)原式=24${x}^{\frac{1}{4}-\frac{1}{2}+\frac{1}{4}}•{y}^{-\frac{1}{3}+\frac{2}{3}+\frac{2}{3}}$=24x0y1=24y.
点评 本题主要考查集合的基本运算以及指数幂的计算,比较基础.

练习册系列答案
相关题目
16.若tanθ=$\frac{1}{3}$,则cos2θ=( )
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{5}{12}$ | D. | $\frac{3}{4}$ |
14.在图所示的程序框图中,若输入x=28,则输出的k=( )


| A. | 4 | B. | 3 | C. | 2 | D. | 5 |
16.下列叙述不正确的是( )
| A. | 无穷小量与无穷大量的商为无穷小量 | |
| B. | 无穷小量与有界量的积是无穷小量 | |
| C. | 无穷大量与有界量的积是无穷大量 | |
| D. | 无穷大量与无穷大量的积是无穷大量 |
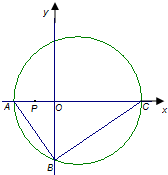 如图,直角三角形ABC的顶点坐标A(-2,0),直角顶点$B(0,-2\sqrt{2})$,顶点C在x轴上,点P为线段OA的中点.
如图,直角三角形ABC的顶点坐标A(-2,0),直角顶点$B(0,-2\sqrt{2})$,顶点C在x轴上,点P为线段OA的中点.