题目内容
18.若关于x的方程x2-x+a-4=0的一根大于零、另一根小于零,求实数a的取值范围.分析 设f(x)=x2-x+a-4,则由题意可得f(0)=a-4<0,由此求得实数a的取值范围.
解答 解:设f(x)=x2-x+a-4,则由题意可得f(0)=a-4<0,
求得a<4.
点评 本题主要考查一元二次方程根的分布与系数的关系,二次函数的性质,体现了转化的数学思想,属于基础题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
10.已知函数f(x)=log2(x2+1),函数g(x)=($\frac{1}{3}$)x-m.若?x1∈[0,3],?x2∈[1,2],使得f(x1)≥g(x2),则m的取值范围是( )
| A. | [$\frac{1}{9}$,+∞) | B. | [$\frac{1}{3}$,+∞) | C. | (-∞,$\frac{1}{9}$] | D. | (-∞,$\frac{1}{3}$] |
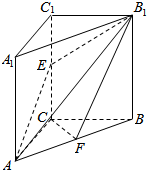 已知在三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,∠ACB=90°,E是棱CC1上的动点,F是AB的中点,AC=1,BC=2,AA1=4.当E为CC1中点时,
已知在三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,∠ACB=90°,E是棱CC1上的动点,F是AB的中点,AC=1,BC=2,AA1=4.当E为CC1中点时, 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点为F(1,0),点(-1,$\frac{\sqrt{2}}{2}$)在椭圆C上,点T满足$\overrightarrow{OT}$=$\frac{{a}^{2}}{\sqrt{{a}^{2}-{b}^{2}}}$•$\overrightarrow{OF}$(其中O为坐标原点),过点F作一斜率为1的直线交椭圆于P、Q两点(其中P点在x轴上方,Q点在x轴下方)
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点为F(1,0),点(-1,$\frac{\sqrt{2}}{2}$)在椭圆C上,点T满足$\overrightarrow{OT}$=$\frac{{a}^{2}}{\sqrt{{a}^{2}-{b}^{2}}}$•$\overrightarrow{OF}$(其中O为坐标原点),过点F作一斜率为1的直线交椭圆于P、Q两点(其中P点在x轴上方,Q点在x轴下方)