题目内容
9.点P(x,y)在椭圆$\frac{x^2}{16}+\frac{y^2}{9}=1$上,则x+y的最大值为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 利用椭圆的参数方程,利用辅助角公式及正弦函数的性质,即可求得x+y的最大值.
解答 解:由题意点P(x,y)在椭圆$\frac{x^2}{16}+\frac{y^2}{9}=1$上,则x=4cosα,y=3sinα,
∴x+y=4cosα+3sinα=5sin(α+φ),tanφ=$\frac{4}{3}$,
由正弦函数的性质可知:x+y的最大值5,
故选:C.
点评 本题考查椭圆的参数方程,辅助角角公式的应用,正弦函数的性质,考查计算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.下面与角$\frac{23π}{3}$终边相同的角是( )
| A. | $\frac{4}{3}π$ | B. | $\frac{π}{3}$ | C. | $\frac{5π}{3}$ | D. | $\frac{2π}{3}$ |
4.函数f(x)=x2-2x-1,x∈[-3,2]的最大值、最小值分别为( )
| A. | 14,-2 | B. | 14,-1 | C. | 2,-2 | D. | 7,-2 |
1.如图所示,在△ABC中,BD=2CD,若$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AC}=\overrightarrow b$,则$\overrightarrow{AD}$=( )
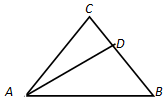

| A. | $\frac{2}{3}\overrightarrow a+\frac{1}{3}\overrightarrow b$ | B. | $\frac{2}{3}\overrightarrow a-\frac{1}{3}\overrightarrow b$ | C. | $\frac{1}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b$ | D. | $\frac{2}{3}\overrightarrow a-\frac{2}{3}\overrightarrow b$ |
