题目内容
点A，B，C，D在同一个球面上，
，AC=2，若球的表面积为
，则四面体ABCD体积最大值为
A． | B． | C． | D．2 |
C
解析试题分析：由题知
，所以∠ABC=90o,设AC中点为E，球的半级为R,过A，B，C三点的截面圆半径
=AE=AC=1，由球的表面积为 知，
=，解得R=
，所以球心到过A，B，C三点的截面
，则
=
，因△ABC的面积为
=1，所以要四面体ABCD体积最大，则D为直线DE与球的交点且球心在线段DE上，所以DE=+=2，所以四面体ABCD体积最大值为
=，故选C．
考点：球的体积
练习册系列答案
相关题目
．
；
的定义域为
，求实数
的取值范围．
+
+
≥ 
＋b
+
+
≥1面积为4的正方形，绕其一边旋转一周，则所得几何体的侧面积为（ ）
A．4 | B．8 | C．12 | D．16 |
中，已知
,
，此三棱柱各个顶点都在一个球面上，则球的体积为（ ）.
，则点P的轨迹周长为( ).
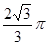
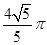
且
，
为大于1的自然数，
；不等式选讲
为正实数，且
，求
的最小值及取得最小值时