题目内容
球O为边长为2的正方体ABCD-A1B1C1D1的内切球,P为球O的球面上动点,M为B1C1中点, ,则点P的轨迹周长为( ).
,则点P的轨迹周长为( ).
A. | B.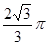 | C. | D.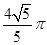 |
D.
解析试题分析:由已知,要有 ,利用三垂线定理,只需考虑
,利用三垂线定理,只需考虑 在平面
在平面 的射影
的射影 与
与 垂直,由平面几何知识可知
垂直,由平面几何知识可知 为
为 的中点,如图2所示,此时,
的中点,如图2所示,此时,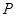 的轨迹即为过
的轨迹即为过 与平面
与平面 垂直的平面
垂直的平面 与球O面相交截得的圆,此时球心O到此圆面的距离即为
与球O面相交截得的圆,此时球心O到此圆面的距离即为 到
到 的距离
的距离 ,由正方体的边长为2,如图3,
,由正方体的边长为2,如图3, 与
与 ,可得
,可得 ,在
,在 中,
中, 为
为 的中点,
的中点, ,所以
,所以 =
= ,即球心O到此圆面的距离为
,即球心O到此圆面的距离为 ,又球O的半径为1,所以圆(
,又球O的半径为1,所以圆(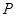 的轨迹)的半径为
的轨迹)的半径为 ,因此所求P的轨迹周长(即为此圆的周长)为
,因此所求P的轨迹周长(即为此圆的周长)为
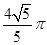 .
.

(图1) (图2)
(图3)
考点:三垂线定理,三角形相似的性质,球的截面性质(球的半径,球心到截面圆心的距离,截面圆的半径三者构成勾股定理关系),圆的周长公式,化归思想.

练习册系列答案
相关题目
点A,B,C,D在同一个球面上, ,AC=2,若球的表面积为
,AC=2,若球的表面积为 ,则四面体ABCD体积最大值为
,则四面体ABCD体积最大值为
A. | B. | C. | D.2 |
某四面体的三视图如图所示,该四面体四个面的面积中最大的是( )
| A.8 | B.6 | C.10 | D.8 |
如图(1)、(2)、(3)、(4)为四个几何体的三视图,根据三视图可以判断这四个几何体依次分别为( )
| A.三棱台、三棱柱、圆锥、圆台 | B.三棱台、三棱锥、圆锥、圆台 |
| C.三棱柱、四棱锥、圆锥、圆台 | D.三棱柱、三棱台、圆锥、圆台 |
棱长为 的正方体内切一球,该球的表面积为( )
的正方体内切一球,该球的表面积为( )
A. | B.2 | C.3 | D. |
某几何体的三视图如图所示,则它的体积是( )
| A.8-2π | B.8- | C.8- | D. |
 ,证明:
,证明: .
.
