题目内容
17.椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),A,B是椭圆与x轴的两个交点,M为椭圆C的上顶点,设直线MA的斜率为k1,直线MB的斜率为k2,k1k2=-$\frac{2}{3}$(Ⅰ)求椭圆C的离心率;
(Ⅱ)设直线l与x轴交于点D(-$\sqrt{3}$,0),交椭圆于P、Q两点,且满足$\overrightarrow{DP}$=3$\overrightarrow{QD}$,当△OPQ的面积最大时,求椭圆C的方程.
分析 (Ⅰ)由题意可得M(0,b),A(-a,0),B(a,0).由斜率公式可得k1,k2,再由条件结合离心率公式计算即可得到所求;
(Ⅱ)由(Ⅰ)知e=$\frac{c}{a}$=$\frac{\sqrt{3}}{3}$,得a2=3c2,b2=2c2,可设椭圆C的方程为:2x2+3y2=6c2,设直线l的方程为:x=my-$\sqrt{3}$,直线l与椭圆交于P,Q两点,联立方程,运用判别式大于0和韦达定理,结合向量共线的坐标表示,求得S△OPQ,化简运用基本不等式可得最大值,进而得到a,b,c,即有椭圆方程.
解答 解:(Ⅰ)由题意可得M(0,b),A(-a,0),B(a,0).
k1=$\frac{b}{a}$,k2=-$\frac{b}{a}$
k1k2=-$\frac{{b}^{2}}{{a}^{2}}$=-$\frac{2}{3}$,b=$\frac{\sqrt{6}}{3}$a,
可得e=$\frac{c}{a}$=$\frac{\sqrt{3}}{3}$.
(Ⅱ)由(Ⅰ)知e=$\frac{c}{a}$=$\frac{\sqrt{3}}{3}$,得a2=3c2,b2=2c2,
可设椭圆C的方程为:2x2+3y2=6c2,
设直线l的方程为:x=my-$\sqrt{3}$,直线l与椭圆交于P,Q两点
$\left\{\begin{array}{l}{x=my-\sqrt{3}}\\{2{x}^{2}+3{y}^{2}=6{c}^{2}}\end{array}\right.$得(2m2+3)y2-4$\sqrt{3}$my+6-6c2=0,
因为直线l与椭圆C相交,所以△=48m2-4(2m2+3)(6-6c2)>0,
由韦达定理:y1+y2=$\frac{4\sqrt{3}m}{3+2{m}^{2}}$,y1y2=$\frac{6-6{c}^{2}}{3+2{m}^{2}}$.
又$\overrightarrow{DP}$=3$\overrightarrow{QD}$,所以y1=-3y2,
代入上述两式有:6-6c2=-$\frac{36{m}^{2}}{2{m}^{2}+3}$,
所以S△OPQ=$\frac{1}{2}$|OD|•|y1-y2|=$\frac{\sqrt{3}}{2}$|$\frac{8\sqrt{3}m}{3+2{m}^{2}}$|
=12•$\frac{|m|}{2|m{|}^{2}+3}$=12•$\frac{1}{2|m|+\frac{3}{|m|}}$≤12•$\frac{1}{2\sqrt{6}}$=$\sqrt{6}$,
当且仅当m2=$\frac{3}{2}$时,等号成立,
此时c2=$\frac{5}{2}$,
代入△,有△>0成立,
所以椭圆C的方程为:$\frac{2{x}^{2}}{15}$+$\frac{{y}^{2}}{5}$=1.
点评 本题考查椭圆的离心率的求法,注意运用直线的斜率公式,考查椭圆的方程的求法,注意运用直线和椭圆方程联立,运用韦达定理和判别式大于0,以及向量共线的坐标表示,和基本不等式,考查化简整理的运算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | {x|x≠±1} | B. | (-∞,-1)∪(1,+∞) | C. | (-1,1) | D. | (-1,0)∪(0,1) |
| A. | $\frac{5}{6}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
| A. | (7,$\frac{29}{4}$) | B. | (21,$\frac{135}{4}$) | C. | [27,30) | D. | (27,$\frac{135}{4}$) |
| A. | {-1,0,1} | B. | {0} | C. | {1} | D. | ∅ |
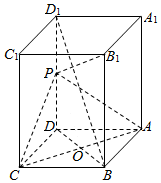 如图,长方体ABCD-A1B1C1D1中,AB=AD=1,点P为DD1的中点.
如图,长方体ABCD-A1B1C1D1中,AB=AD=1,点P为DD1的中点.