题目内容
20.己知函数f(x)=2-|x|.(1)把函数y=f(x)写成分段函数的形式,并作出其大致图象;
(2)根据图象写出其单调区间和值域;
(3)若方程2-|x-1|=a有两个解,求实数a的取值范围.
分析 (1)去掉绝对值,可把函数y=f(x)写成分段函数的形式,并作出其大致图象;
(2)根据图象,即可写出其单调区间和值域;
(3)y=2-|x-1|的图象是由f(x)=2-|x|的图象向右平移1个单位,利用方程2-|x-1|=a有两个解,求实数a的取值范围.
解答 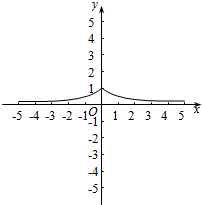 解:(1)f(x)=2-|x|=$\left\{\begin{array}{l}{{2}^{-x},x≥0}\\{{2}^{x},x<0}\end{array}\right.$,如图所示;
解:(1)f(x)=2-|x|=$\left\{\begin{array}{l}{{2}^{-x},x≥0}\\{{2}^{x},x<0}\end{array}\right.$,如图所示;
(2)单调增区间是(-∞,0),单调减区间是(0,+∞),值域是(0,1];
(3)y=2-|x-1|的图象是由f(x)=2-|x|的图象向右平移1个单位.
∵方程2-|x-1|=a有两个解,
∴0<a<1.
点评 本题考查函数的解析式,考查函数的图象,正确做出函数的图象是关键.

练习册系列答案
相关题目
11.已知x,y取值如表:
画散点图可知:y与x线性相关,且求得回归线方程为$\widehat{y}$=$\widehat{x}$+1,则m的值为1.7(精确到0.1)
| x | 0 | 1 | 4 | 5 | 6 |
| y | 1.3 | m | 3m | 5.6 | 7.4 |
9.已知函数f(x)=x2+ax的图象在点A(0,f(0))处的切线l与直线2x-y+2=0平行,若数列{$\frac{1}{f(n)}$}的前n项和为Sn,则S20的值为 ( )
| A. | $\frac{325}{462}$ | B. | $\frac{19}{20}$ | C. | $\frac{119}{256}$ | D. | $\frac{2010}{2011}$ |
10.下列各函数中,其图象经过点(1,0)的是( )
| A. | y=x2+1 | B. | y=$\frac{1}{x}$ | C. | y=3x | D. | y=lgx |