题目内容
若ax+2a+1＞0在0≤a≤1时恒成立，求x取值范围．
考点：函数恒成立问题
专题：不等式的解法及应用
分析：分a=0和a≠0两种情况讨论，对于后者将不等式转化为x＞-2-
．根据a的范围确定-2-
≤-3，从而可得x取值范围是（-3，+∞）．
| 1 |
| a |
| 1 |
| a |
解答：
解：当a=0时，不等式ax+2a+1＞0显然成立．
当a≠0时，不等式ax+2a+1＞0可化为
x＞-2-
．
∵0＜a≤1，
∴
≥1．
∴-2-
≤-3．
∴ax+2a+1＞0在0≤a≤1时恒成立等价于
x＞-3，
∴x取值范围是（-3，+∞）．
当a≠0时，不等式ax+2a+1＞0可化为
x＞-2-
| 1 |
| a |
∵0＜a≤1，
∴
| 1 |
| a |
∴-2-
| 1 |
| a |
∴ax+2a+1＞0在0≤a≤1时恒成立等价于
x＞-3，
∴x取值范围是（-3，+∞）．
点评：本题考查分情况讨论的数学思想和不等式性质的应用，属于中档题．
练习册系列答案
一卷搞定系列答案
名校作业本系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
若cosα=
，则
=（ ）
| ||
| 4 |
| tanα |
| cos(π-α) |
A、±4
| ||||
B、±2
| ||||
C、-
| ||||
D、
|
全称命题“?x∈R，x2+9x=4”的否定是（ ）
| A、?x0∈R，x02+9x0≠4 |
| B、?x∈R，x2+9x≠4 |
| C、?x0∈R，x02+9x0=4 |
| D、以上都不正确 |
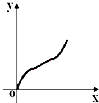
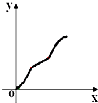
如图，不规则图形ABCD中：AB和CD是线段，AD和BC是圆弧，直线l⊥AB于E，当l从左至右移动（与线段AB有公共点）时，把四边形ABCD分成两部分，设AE=x，左侧部分面积为y，则y关于x的大致图象为（ ）
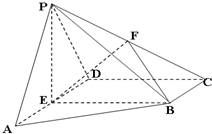已知在四棱锥P-ABCD中，AD∥BC，AD⊥CD，PA=PD=AD=2BC=2CD，E，F分别是AD，PC的中点．
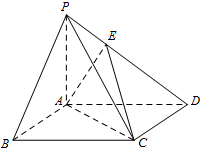如图：在四棱锥P-ABCD中，底面ABCD是正方形，PA=AB=2，PB=PD=2