题目内容
【题目】已知函数f（x）= 
（x＞0），m∈R．
（1）若函数f（x）有零点，求实数m的取值范围；
（2）若函数f（x）的图象在点（1，f（x））处的切线的斜率为 
，且函数f（x）的最大值为M，求证：1＜M＜ 
．
【答案】
（1）解：若函数f（x）有零点，
则f（x）=0有解，
即m 
+lnx=0有解，
即有﹣m= 
，
由g（x）= 的导数为g′（x）= 
，
当x＞e2时，g′（x）＜0，g（x）递减；
当0＜x＜e2时，g′（x）＞0，g（x）递增．
可得g（x）在x=e2时，取得极大值，且为最大值 
，
可得﹣m＞ ，解得m＜﹣ ，
则实数m的取值范围为（﹣∞，﹣ ）
（2）证明：函数f（x）= 
（x＞0）的导数为f′（x）=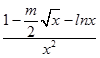 
，
可得f（x）在点（1，f（1））处的切线的斜率为1﹣ 
= 
，
解得m=1，
即有f（x）= 
的导数为f′（x）=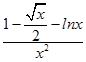 
，
令f′（x）=0，可得lnx+ 
=1，
设方程的解为t，由h（x）=lnx+ ﹣1递增，且h（1）﹣1=﹣ ＜0，h（ 
）=ln + 
﹣1＞0，
可得1＜t＜ ，且lnt+ 
=1，
即有f（x）的最大值为f（t）= 
= 
= 
+ 
=（ 
+ 
）2﹣ 
，
可得f（t）在（1， ）递减，
f（1）= ，f（ ）= 
+ 
＞1，
即有f（t）∈（f（ ），f（1）），
则有1＜M＜
【解析】（1）由题意可得f（x）=0有解，即m 
+lnx=0有解，即有﹣m= 
，设g（x）= ，求得导数和单调区间，可得极大值，且为最大值，即可得到m的范围；（2）求出f（x）的导数，求得切线的斜率，可得m=1，再令f′（x）=0，设出极大值点，也即最大值点，运用函数零点存在定理，可得t的范围，化简整理由二次函数的单调性，即可得证．
【考点精析】通过灵活运用利用导数研究函数的单调性，掌握一般的,函数的单调性与其导数的正负有如下关系： 在某个区间
内，(1)如果
，那么函数
在这个区间单调递增；(2)如果
，那么函数
在这个区间单调递减即可以解答此题．
