题目内容
2.已知集合M={(x,y)|y=f(x)},若对于任意实数对(x1,yl)∈M,存在(x2,y2)∈M,使得x1x2+y1y2=0成立,则称集合M为“正交点集”,给出下列集合;①M={(x,y)|y=$\frac{1}{x}$};②M={(x,y)|y=-x2+1};③M={(x,y)|y=cosx};
④M={(x,y)|y=x-$\frac{1}{x}$);⑤M={(x,y)||x|+|y|=1}.
则满足条件的“正交集合”有:②③⑤(写出所有满足条件的集合的序号)
分析 ①对于任意实数对(x1,yl)∈M,则x1y1=1,因此不存在(x2,y2)∈M,使得x1x2+y1y2=0成立,即可判断出正误;
②对于任意实数对(x1,yl)∈M,假设存在(x2,y2)∈M,使得x1x2+y1y2=0成立,则x1x2+$(1-{x}_{1}^{2})(1-{x}_{2}^{2})$=0,化为:$({x}_{1}^{2}-1){x}_{2}^{2}$+x1x2-$({x}_{1}^{2}-1)$=0,当x1=±1时,(±1,0),则存在(0,1),满足x1x2+y1y2=0;当x1≠±1时,△>0,因此存在(x2,y2)∈M,满足x1x2+y1y2=0,即可判断出正误;
③M={(x,y)|y=cosx},如图所示:任取点P,则存在点Q,使得OP⊥OQ,即可判断出正误.
④取(1,0),则不存在(x2,y2)(x2≠0)∈M,使得x1x2+y1y2=x2=0成立,即可判断出正误;
⑤M={(x,y)||x|+|y|=1},由图象可知:任取点P,则在图象上存在点Q,使得OQ⊥OP,即可判断出正误.
解答 解:①M={(x,y)|y=$\frac{1}{x}$},对于任意实数对(x1,yl)∈M,则x1y1=1,因此不存在(x2,y2)∈M,使得x1x2+y1y2=0成立,不正确;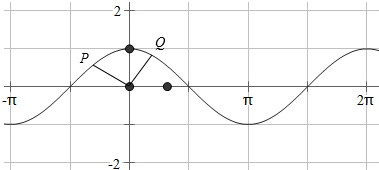
②M={(x,y)|y=-x2+1},对于任意实数对(x1,yl)∈M,假设存在(x2,y2)∈M,
使得x1x2+y1y2=0成立,则x1x2+$(1-{x}_{1}^{2})(1-{x}_{2}^{2})$=0,化为:$({x}_{1}^{2}-1){x}_{2}^{2}$+x1x2-$({x}_{1}^{2}-1)$=0,当x1=±1时,(±1,0),则存在(0,1),满足x1x2+y1y2=0;
当x1≠±1时,△=${x}_{1}^{2}$+4$({x}_{1}^{2}-1)^{2}$>0,因此存在(x2,y2)∈M,满足x1x2+y1y2=0,
∴M是“正交集合”;
③M={(x,y)|y=cosx},如图所示:任取点P,则存在点Q,使得OP⊥OQ.
因此对于任意实数对(x1,yl)∈M,存在(x2,y2)∈M,使得x1x2+y1y2=0成立,因此集合M是“正交集合”,正确;
④M={(x,y)|y=x-$\frac{1}{x}$),取(1,0),则不存在(x2,y2)(x2≠0)∈M,使得x1x2+y1y2=x2=0成立,因此不正确;
⑤M={(x,y)||x|+|y|=1},由图象可知:任取点P,则在图象上存在点Q,使得OQ⊥OP.即对于任意实数对(x1,yl)∈M,存在(x2,y2)∈M,使得x1x2+y1y2=0成立,∴集合M是“正交集合”,因此正确.
则满足条件的“正交集合”有:②③⑤.
故答案为:②③⑤.
点评 本题考查了新定义“正交集合”的性质、向量垂直与数量积的运算性质,考查了数形结合方法、推理能力与计算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | 7 | B. | 15 | C. | 35 | D. | 21 |
| A. | $\frac{1}{7}$ | B. | $\frac{2}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{4}{7}$ |