题目内容
14.已知函数f(x)对任意实数x均有f(x)=kf(x+2),其中常数k为负数,且f(x)在区间[0,2]有表达式f(x)=x(x-2)(I)求出f(-1),f(2.5)的值;
(Ⅱ)若函数f(x)在区间[-2,2]的最大值与最小值分别为m,n,且m-n=3,求k的值.
分析 (1)直接根据定义得f(x+2)=$\frac{1}{k}$f(x),求得f(2.5)和f(-1);
(2)先求出f(x)的解析式f(x)=$\left\{\begin{array}{l}{x(x-2),x∈[0,2]}\\{kx(x+2),x∈[-2,0)}\end{array}\right.$,再求出各分段的值域,得出m,n的值.
解答 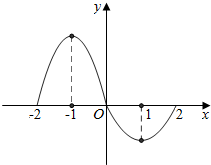 解:(1)因为f(x)=kf(x+2),
解:(1)因为f(x)=kf(x+2),
所以,f(x+2)=$\frac{1}{k}$f(x),因此,
f(2.5)=$\frac{1}{k}$f(0.5)=-$\frac{9}{4k}$,
f(-1)=kf(1)=-k;
(2)根据题意,当x∈[0,2],f(x)=x(x-2),
当x∈[-2,0]时,x+2∈[0,2],
所以f(x)=kf(x+2)=k(x+2)x,其中,k<0,
因此,x∈[-2,2]时,f(x)=$\left\{\begin{array}{l}{x(x-2),x∈[0,2]}\\{kx(x+2),x∈[-2,0)}\end{array}\right.$,
当x∈[0,2],f(x)=(x-1)2-1∈[-1,0],
当x∈[-2,0],f(x)=k[(x+1)2-1]∈[0,-k],
所以,函数的最大值为m=-k,最小值为n=-1,如右图,
因为,m-n=3,-k+1=3,
解得k=-2.
点评 本题主要考查了函数值的求解,分段函数解析式的确定,以及运用二次函数的性质确定函数的值域,属于中档题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
19.给出如下四个判断:
①?x0∈R.ex0≤0;③设a,b是实数,a>1,b>1是ab>1的充要条件;
②?x∈R+,2x>x2;④命题“若p则q”的逆否命题是若¬q,则¬p.
其中正确的判断个数是( )
①?x0∈R.ex0≤0;③设a,b是实数,a>1,b>1是ab>1的充要条件;
②?x∈R+,2x>x2;④命题“若p则q”的逆否命题是若¬q,则¬p.
其中正确的判断个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
6.设集合M={y|y=x2},N={x|y=$\sqrt{{x}^{2}+2x+1}$},则M∩N为( )
| A. | M?N | B. | M?N | C. | M=N | D. | M∩N=∅ |
3.函数f(x)是奇函数,且对于任意的x∈R都有f(x+2)=f(x),若f(0.5)=-1,则f(7.5)=( )
| A. | -1 | B. | 0 | C. | 0.5 | D. | 1 |
4.a,b∈R,且a+2b=2,则2a+4b的最小值是( )
| A. | 24 | B. | 16 | C. | 8 | D. | 4 |